Los mapeos globales derivados por los mapeos locales restringidos por una 
partícular ofrecen un nuevo
enfoque de estudio basado en las mismas configuraciones 
. Si 
es una cadena de longitud lg(x)=l, entonces 
es un estado global.
Con esta definición podemos contruir un nuevo diagrama, conocido como diagrama de
transiciones [13]. Estos diagramas de
transiciones estan formados por todos los estados globales del conjunto de 
. Si l representa el
tamaño de una configuración 
, entonces tenemos 
estados globales. Estos diagramas de transiciones también son conocidos como
árboles topólogicos [18] donde cada nodo representa
un estado global y las flechas indican la transición en un paso. Se tiene una raíz
cíclica formada por uno o más estados globales, de esta raíz se desprenden ramas
formadas por las mismas transiciones y finalmente estas ramas contienen hojas donde estas
hojas representan la configuración inicial (para algunos casos) del diagrama de
evoluciones. La función de transición que determina un mapeo global se representa como:
Como se había señalado los nodos de tal gráfica son las configuraciones finitas de
tamaño l. Si tenemos un autómata con k = 2 y r = 1 podemos formar
configuraciones de tamaño 
para alguna 
.
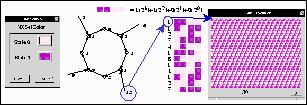
Figura 3.8: Transiciones globales.
Los valores que toman cada uno de los nodos dentro del diagrama de transiciones se
obtienen a través de la suma de los valores de cada una de las células múltiplicadas
por su potencia correspondiente a la posición que ocupan cada una de ellas. Si tenemos un
autómata binario con k = 2, r = 1 y l = 4, entonces tenemos 
posibles configuraciones
formadas por elementos que pertenecen a 
. Para este caso son 16 configuraciones de tamaño cuatro que pertenencen al
conjunto 
.
