

Next: Autómatas celulares con Up:
Algunos algoritmos existentes Previous:
Algoritmo de Fredkin
Hillman [20] hace notar que los autómatas
celulares reversibles no sólo dependen de la regla de evolución, si no que hay otros
factores que intervienen en tal proceso y este es el caso del tamaño del anillo de
evolución.
Sea C una cadena de x células en el tiempo t, de este modo C
está completamente determinado por la cadena de células P de longitud x+d-1
en el tiempo t-1, donde d es el tamaño de la vecindad del autómata.
- Si
 es una configuración
en C, sea
es una configuración
en C, sea 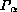 el
conjunto de configuraciones las cuales de acuerdo a una regla de evolución dada generan
el
conjunto de configuraciones las cuales de acuerdo a una regla de evolución dada generan  .
.
- Sea
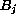 la j-ésima
configuración presente en
la j-ésima
configuración presente en 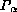 ,
entonces formamos una tabla
,
entonces formamos una tabla 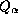 la cual su j-ésimo elemento será igual a
la cual su j-ésimo elemento será igual a 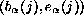 , donde
, donde 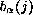 es el conjunto de las primeras d-1 células en
es el conjunto de las primeras d-1 células en 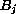 y
y 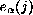 es el conjunto de las últimas d-1
células en
es el conjunto de las últimas d-1
células en 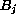 .
.
- Finalmente formamos
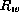 como el conjunto de todas las tablas posibles
como el conjunto de todas las tablas posibles 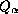 dado un ancho w especificado. Si w>1 entonces
dado un ancho w especificado. Si w>1 entonces 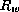 se obtiene de la
concatenación de
se obtiene de la
concatenación de 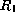 y
y 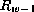 para cada elemento
para cada elemento 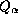 de
de 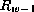 y
y 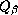 de
de 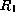 ,
uno obtiene un elemento
,
uno obtiene un elemento 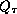 de
de 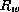 después de comparar
cada entrada
después de comparar
cada entrada 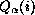 con cada
entrada
con cada
entrada 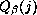 , si
, si 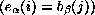 entonces añadimos a
entonces añadimos a 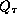 una entrada m tal que
una entrada m tal que 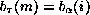 y
y 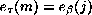 . El proceso recursivo empieza calculando
. El proceso recursivo empieza calculando 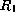 directamente de la regla de
evolución.
directamente de la regla de
evolución.
- Los elementos
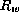 contienen
tablas
contienen
tablas 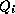 con las listas de
las primeras y las últimas d-1 células de cada ancestro de una cadena de longitud
w especificada. Las primeras d-1 células deben ser iguales a las últimas d-1
células si existe un ancestro, ya que su ancho será de w+d-1. Así el j-ésimo
ancestro existirá si y sólo si
con las listas de
las primeras y las últimas d-1 células de cada ancestro de una cadena de longitud
w especificada. Las primeras d-1 células deben ser iguales a las últimas d-1
células si existe un ancestro, ya que su ancho será de w+d-1. Así el j-ésimo
ancestro existirá si y sólo si 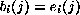 . Por lo tanto, si el autómata es reversible cada tabla
. Por lo tanto, si el autómata es reversible cada tabla 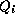 debe tener una y sólo una entrada j
tal que
debe tener una y sólo una entrada j
tal que 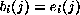 .
.
- El algoritmo para hasta un ancho w especificado.


Next: Autómatas celulares con Up:
Algunos algoritmos existentes Previous:
Algoritmo de Fredkin
Genaro Juárez Martínez
E-mail:genaro@sparcomp.cs.cinvestav.mx
![]()
![]()