El autómata celular (2,1) regla 45 presenta grados de reversibilidad para
configuraciones de tamaño impar, tomamos este autómata como un ejemplo práctico ya que
para mostrar de manera detallada estas propiedades para el autómata 
el trabajo es demasiado laborioso y poco
práctico, siendo que la finalidad es la misma para todos los casos.
La matriz de de Bruijn simbólica para el autómata (2,1) presentada en la Sección 4.3.1, es general para todo autómata con estos valores, ya que sus elementos son las mismas vecindades que forman la regla de evolución.
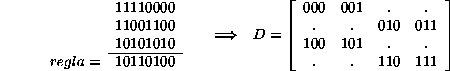
Ahora bien sabemos de antemano que este autómata posee un mapeo suryectivo, es decir carece de configuraciones pertenecientes al Jardín del Edén y tiene múltiples ancestros. Sin embargo lo curioso de esta regla es que tiene comportamientos reversibles para configuraciones de tamaño impar y para que esta propiedad se cumpla es necesario que el autómata posea un mapeo biyectivo, o sea que tenga un único ancestro por cada configuración.
Si construimos una tabla de vecindades para obtener sus respectivas células de
evolución, estas vecindades estan denotadas por 
posibles combinaciones, para obtener configuraciones de longitud 
.
Tabla 4.1: Tabla de evoluciones con 
y 
.
Si r=1 entonces tenemos 
posibles bloques de evoluciones, si 
entonces tenemos 16 posibles bloques y así sucesivamente. El
crecimiento es por demás exponencial, si hubieramos trabajado con el autómata 
los valores por columna serian
64, 256, 1024 y 4096 respectivamente. Por lo que el estudio hubiera sido muy laborioso por
realizar.
Para el caso cuando r=1 tenemos que sus bloques de evoluciones coinciden con las mismas vecindades del autómata y sus respectivas células de evolución; se puede observar que en este caso existen igual número de ceros y de unos en las células de evolución de estos bloques. A esta propiedad se le conoce como múltiplicidad uniforme, esto es cada uno de los estados tiene el mismo número de imágenes que los demás estados que conforman el autómata celular.
En este caso el estado cero tiene cuatro imágenes y el estado uno también,
Tabla 4.2: Configuraciones con l=1.
esto quiere decir que con las cadenas 001, 100, 110 y 111 podemos construir un 0 en la siguiente generación. Ahora bien si las dos células de la izquierda coinciden con las dos células de la derecha podemos translapar estas células con la finalidad de determinar que configuración es un posible ancestro de las células de evolución en los estados globales.
Este concepto es más visible para configuraciones de tamaño mayor igual que dos, ya que podemos formar bloques de evoluciones de tamaño cuatro y obtener configuraciones de tamaño dos con sus respectivas transiciones.
Tabla 4.3: Configuraciones con l=2.
Como podemos observar en la Tabla 4.3 para las células de evolución 00 el bloque 1111 cumple con la condición de tener la misma pareja de estados en la izquierda como en la derecha, por lo que deducimos que la configuración 00 tiene un ancestro formado por la cadena 11.
Ls Figura 4.2 ilustra paso a paso como formamos las configuraciones globales a partir de los bloques de evoluciones; la cadena 00 tiene cuatro imágenes pero la imagen 1111 tienen los estados 11 a la izquierda del bloque y 11 a la derecha del mismo bloque, por lo que definimos su traslape si
Si analizamos las células de evolución para la cadena 11 de la Tabla 4.3 podemos notar que tal configuración tiene tres bloques de evolución que cumplen con dicha condición, estos bloques son 1010, 0101 y 0000. Lo que implicaría que los estados globales 2, 1 y 0 mapean al estado global 3. De esta manera podemos obtener todos los ancestros de cada uno de los bloques de evolución que podemos formar con r.
Para comprobar nuestros resultados construyamos su respectivo árbol topológico y revisemos cada uno de sus mapeos posibles.
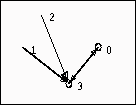
Figura 4.3: Árbol topológico con l=2.
Finalmente podemos comprobar que cuando l=2 las configuraciones 
tienen más de un ancestro. El
estado 0 mapea al estado 3 y el estado 3 mapea al estado 0 formando la raíz cíclica de
dicho árbol topológico. El estado 2 mapeo al estado 3 y el estado 1 también mapea al
estado 3, por lo que los estados 1 y 2 forman hojas dentro del árbol topológico y no
tienen ancestros cuando l=2.
Ahora analizemos el caso cuando l=3 revisando sus respectivos bloques de evolución calculados en la Tabla 4.1,
Tabla 4.4: Configuraciones con l=3.
nuevamente todas las células de evolución tienen el mismo número de bloques que
producen dichas cadenas. Pero en este caso todas las configuraciones tienen una sola
imagen, estas son: 
, 
, 
, 
, 
,
, 
y 
respectivamente.
Esto significa que tenemos ciclos de tamaño uno, dos y tres, dentro de los árboles
topológicos cuando l=3. Los ciclos de longitud igual a uno estan formados por los
estado globales 
, 
y 
. El ciclo de longitud igual a dos esta formado
por los estados globales 
.
El ciclo de longitud igual a tres esta formado por los estados globales 
, 
y 
.
Figura 4.4: Árboles topológicos con l=3.
La Figura 4.4 muestra todos los estados globales posibles cuando l=3, el
diagrama de transiciones confirma nuestros resultados sobre los ciclos calculados con los
bloques de evoluciones, donde habíamos obtenido cinco ciclos en total. Como señalamos en
la Sección 4.1 los autómatas celulares reversibles deben de tener un mapeo biyectivo que
implica que no tengan múltiples ancestros y támpoco configuraciones pertenecientes al
Jardín del Edén. Esta condición se cumple para este autómata cuando la longitud de 
es de tamaño impar.
Para confirmar nuestra afirmación realizaremos el cálculo de los bloques de evolución cuando l es igual a cinco, siete y nueve. Comprobando que tienen grados de reversibilidad para todos sus árboles topológicos de este tamaño.
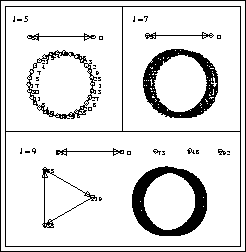
Figura 4.5: Árboles topológicos con l=5, 7 y 9.
Podemos ver que si l=5 el cálculo se hace un poco laborioso, si l=7 el cálculo se hace más laborioso y si l=9 el cálculo es sumamente complicado. Sin embargo todas estas configuraciones son reversibles en todos sus árboles topológicos posibles.
