El autómata celular 
regla 0056B9EF presenta grados de reversibilidad para configuraciones de ancho impar. La
notación Wolfram para el caso 
dentro de la regla de evolución se representa de la siguiente manera:
Tabla 4.5: Regla de evolución.
las vecindades se agrupan de dos en dos y se múltiplican por sus respectivas potencias de acuerdo a la posición que ocupen sobre la misma regla, finalmente se suman estas parejas y se obtiene el número Wolfram.
Para construir los bloques de evoluciones para el autómata (2,1) cuando 
estos se realizaron de forma
manual obteniendo sus células de evolución de acuerdo a una regla dada. En el caso del
autómata 
es aún más
laborioso construir cada uno de estos bloques conforme r se va incrementando. Para
resolver este problema haremos uso de las matrices de conectividad, con lo que obtendremos
los mismos resultados para una l específica.
La matriz simbólica de de Bruijn para el autómata 
se denota de la siguiente manera:
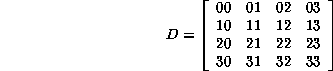
y dada su regla de evolución obtenemos su matriz de evoluciones correspondiente
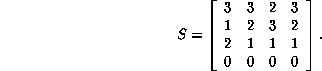
Si efectuamos el producto tensorial de la matriz S obtendremos las siguientes evoluciones
que calcula todos los bloques de evoluciones cuando r=1. Ahora podemos calcular los anillos correspondientes para sus respectivas células de evolución.
Trabajemos con los estado cero y dos, calculando sus bloques de evolución.
Tabla 4.6: Configuraciones con l=2.
En la Tabla 4.6 podemos ver que la configuración 00 tiene un único ancestro formado por la configuración 33, sin embargo la configuración 22 tiene tres ancestros formados por las configuraciones 20, 11 y 02.
La Figura 4.6 muestra las configuraciones por estados globales y su valor decimal para
cada una de ellas. El primer diagrama nos indica que la configuración 33 mapea a la
configuración 00 en un paso, si revisamos la matriz 
podemos ver que el índice (00,00) tiene por
elemento la cadena 33 lo que confirma su mapeo global, sin embargo notemos que el índice
(33,33) tiene por elemento la cadena 00 por lo que deducimos que existe un ciclo de
longitud dos entre las cadenas 00 y 33. El segundo diagrama nos indica que la
configuración 20, 11 y 02 mapean a la configuración 22 en un paso, esto quiere decir que
los índices de la matriz 
(02,20) tienen por elemento la cadena 22, los índices (20,02) tienen por elemento la
cadena 22 y el índice (11,11) tiene por elemento la cadena 22.
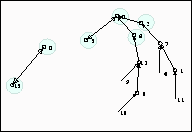
Figura 4.7: Árboles topológicos con l=2.
Los árboles topológicos de la Figura 4.7 confirma nuestros resultados encerrando en
un círculo aquellas configuraciones que calculamos con la matriz 
.
Si deseamos saber especifícamente los ancestros de una configuración en particular
sin calcular toda la matriz 
, podemos obtenerlos a través de un producto matricial dada por la matriz 
.
Analizemos la configuración 22 calculada anteriormente, donde la matriz 
determinará todas las
posibles imágenes que tiene dicha configuración, como podemos observar la matriz 
tiene cuatro imágenes y esto
es por que las configuraciones de tamaño uno son los mismos mapeos de cada una de las
vecindades posibles para la regla en estudio.
Si calculamos la matriz 
obtendremos todas las imágenes posibles de la cadena 22 en un sólo paso, ya que los
índices de las matrices que representan dicho producto, también determinaran las cadenas
de evolución que existen para la cadena 22. Como podemos ver el número de imágenes es
el mismo.
Entonces tenemos cuatro imágenes de tamaño tres y los bloques de evoluciones van a
estar representandos por el valor del renglón y la columna de la primera matriz; con el
valor del renglón que determine el producto de dicho elemento con la segunda matriz. Por
lo que finalmente podemos decir que para la cadena 22 los bloques de evoluciones obtenidos
en la matriz 
estan
representados por: 020, 111, 113 y 202 respectivamente, como habíamos determinado en la
Tabla 4.6.
El diagrama de subconjuntos de este autómata celular muestra que cadenas tienen múltiples ancestros; estas cadenas se identifican por que forman ciclos de longitud mayor igual que uno en las clases unitarias intermedias.
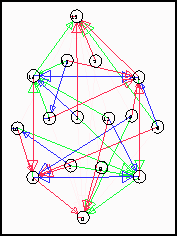
Figura 4.8: Diagrama de subconjuntos de la regla 0056B9EF.
Notemos en la Figura 4.8 que las cadenas formadas por el estado 2 en los nodos 
y 
forman ciclos de longitud dos, el estado dos es
el estado que origina múltiples ancestros de forma inmediata como ilustramos en la Figura
4.6, ya que la cadena 22 por si misma tiene tres ancestros esto quiere decir que para toda
expresión regular formada por las cadenas 22*, esta cadena tiene más de un ancestro.
Ahora veamos la cadena de los nodos 
formada por los estados 13 cuya expresión forma un ciclo que puede ser mayor
igual que dos, esto nos indica que esta cadena tiene más de un ancestro.
Tabla 4.7: Configuraciones con l=2.
La Tabla 4.7 muestra los bloques de evolución para las cadenas 13 y 31, la cadena 13
tiene dos ancestros formados por las cadenas de 01 y 12, lo que equivale que la
configuración 7 tiene por ancestos las configuraciones 1 y 6 como ilustramos en la Figura
4.7. La cadena 31 también forma un ciclo equivalente al de la cadena 13 en los nodos 
, pues es una permutación de
dicha cadena que conserva las mismas propiedades. Finalmente podemos verificar todas estas
múltiplicidades en el diagrama de parejas
Figura 4.9: Diagrama de parejas de la regla 0056B9EF.
Para obtener las configuraciones que forman los ciclos dentro del diagrama de parejas, analizemos el diagrama de parejas de la Figura 4.9 y apartemos algunos casos.
La secuencia formada por los nodos (0,2) y (2,0) debe producir un bloque de evolución que tenga más de un ancestro, construyamos una secuencia de longitud tres dada de la siguiente manera:
si tomamos los elementos de la derecha de cada nodo formamos un bloque de evolución dado por
que a su vez produce las células de evolución 22. Ahora bien si tomamos los elementos de la derecha obtendremos otro ancestro de la cadena 22 denotado de la siguiente manera
por lo que se deduce que la cadena 22 tiene dos ancestros de evolución diferentes, los
bloques 020 y 202 construidos manualmente en la Tabla 4.3 y representado en la Figura 4.6.
Lo mismo sucede para la secuencia de nodos dada por los ciclos 
y 
. Esto significa que podemos obtener todos los ancestros de las
secuencias del diagrama de parejas y a su vez estas secuencias las podemos incrementar de
acuerdo al número de células que queramos analizar en una configuración de longitud l.
Las herramientas gráficas tales como el diagrama de subconjuntos y el diagrama de parejas son de mucha útilidad ya que nos ayudan a verificar nuestros resultados de una manera más rápido y seguro. El diagrama de transiciones reafirma estas propiedades revisando que el mapeo global coincida con los mapeos globales determinados anteriormente.
Finalmente proponemos un método para saber si un autómata celular tiene grados de
reversibilidad o no. Nuestro método se basa en el producto matricial de las matrices de
conectividad por estado del autómata en estudio. Las matrices de conectividad 
para este autómata se
construyen de la siguiente manera:
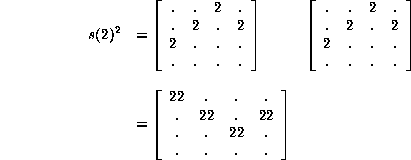
Si elevamos al cuadrado la matriz 
obtendremos el siguiente resultado
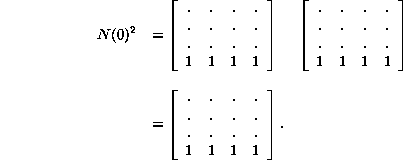
Lo que significa que para toda cadena formada por el estado 0 siempre obtendremos un ancestro único. Si la cadena esta formada por 00* entonces su único ancestro va a estar formado por la cadena 33*. Notemos que este comportamiento es el mismo para los estados 1 y 3.
Donde el único ancestro para la cadena 11* esta formado por la cadena 22*, para la
cadena 33* su único ancestro esta formada por la cadena 00*. Esto implica que la traza de
la matriz debe ser igual a uno: por lo que la 
, la 
y la 
.
Entonces estas configuraciones tendran comportamientos reversibles.
Ahora análicemos la matriz 
cuando k=2,
una vez más podemos verificar que el estado 2 por si mismo tiene tres ancestros en configuraciones de tamaño dos formados por los estados 0, 1 y 2, como lo habíamos señalado en la Tabla 4.6, Figura 4.6 y Figura 4.9. Por lo que deducimos que el estado 2 es el estado que determina los grados de reversibilidad en esta regla.
Para verificar que esto es verdad sólo elevemos la matriz 
sucesivamente.
