Next: Propiedades globales de Up: Propiedades de la Previous: Propiedades de la

Propiedades por cada estado

Primero se definirá que propiedades debe tener cada estado dentro de la matriz de evolución para construir las posibles reglas reversibles.

• Cada estado debe aparecer una sola vez en la diagonal principal

  Esto nos garantiza que cada estado tengan un ancestro, pero si en la diagonal principal existen más de un elemento del mismo estado, se tendrán múltiples formas de ese mismo estado, lo que no puede ocurrir en un ACLR.

   
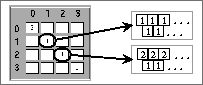
  Figura: ACL(4,h) con múltiples ancestros para una cadena de 1's.
  

  Como se ve en la figura, una secuencia de 1's puede ser construida por una cadena de 1's o de , es decir, tiene varios ancestros posibles lo que no permite que sea reversible.

• Cada estado debe aparecer el mismo número de veces que el resto en la matriz de evolución

  En un ACLR la multiplicidad uniforme de cada cadena debe ser respetada, si en principio un estado puede generarse de un mayor número de maneras que otro estamos contradiciendo este requerimiento.

   
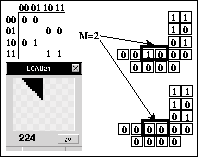
  Figura: ACL(2,1) con múltiples ancestros para una cadena de 0's.
  

  En la figura anterior se observa que una cadena formada de 0's tiene un valor de M=2 debido a que el estado 0 aparece más veces que el estado 1; lo que produce que en la evolución del ACL el estado 1 vaya desapareciendo conforme transcurre el tiempo.

  De esta manera se observa que la multiplicidad uniforme debe cumplirse en la formación de cada estado dentro de la regla de evolución y como se definió en la sección 3, el valor de los posibles ancestros de cada estado debe ser igual a ó al número de nodos del diagrama de de Bruijn.