Una vez definidas que propiedades debe cumplir cada estado en un ACLR, podemos utilizar las mismas para construir solo aquellas matrices de evolución que cumplan dichas propiedades y no todas las posibles reglas; sin embargo, el problema de la reversibilidad en un ACLR también depende de la interacción que los estados tengan unos con otros; esta interacción debe ser tal que permita conservar la información del sistema para poder reconstruir la evolución del mismo ya sea hacia adelante o hacia atrás en el tiempo, esto quiere decir que en un ACLR cada configuración global debe ser posible de generar a través de la evolución del autómata, pero por uno y solo un ancestro posible, evitando que exista el Jardín del Edén o ancestros múltiples.
Para lograr este objetivo se utilizarán los otros dos conceptos importantes expuestos
en [9] y [16], que son
los índices de Welch y la combinabilidad, en realidad estos conceptos están muy
relacionados entre sí ya que la combinabilidad es solo checar que toda ruta posible con
una longitud mayor o igual que 2r tenga los mismos valores de los índices L
y R cumpliendo que 
.
La pregunta aquí es cómo podemos observar ésto en la matriz de evolución de un ACL; en realidad la matriz de evolución puede ser descompuesta en matrices de conectividad, una para cada estado, cada matriz de conectividad tendrá un 1 si exite una liga con el valor de su estado que va de un nodo a otro en el diagrama de de Bruijn.
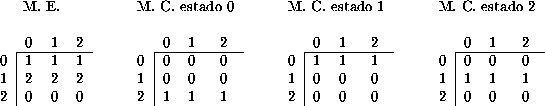
Tabla: Matriz de evolución de ACLR(3,h) regla 715 y sus matrices de
conectividad.
Las matrices de conectividad nos dan también las rutas de tamaño 1 que existen
en el diagrama de de Bruijn y podemos saber si tales rutas cumplen con la propiedad de
combinabilidad examinando la matriz de conectividad para cada estado, por ejemplo, para el
ACLR(3,h) anterior, se observa que para la matriz de conectividad del estado 0
empezando desde el renglón 2 puedo llegar a los estados 0,1 y 2,
es decir el valor de la cardinalidad del conjunto de extensiones compatibles por la
derecha del estado 2 que genere un 0 al evolucionar es 3, como no
puede existir otra cardinalidad mayor por el principio de multiplicidad uniforme se tiene
que R=3; ahora si examinamos en la misma matriz las columnas 0, 1 y 2,
vemos que cada una de éstas son parte final de la liga que empieza desde el renglon 2,
es decir, cada uno de estos estados tiene una cardinalidad del conjunto de extensiones
compatibles por la izquierda igual a 1 para generar un 0, debido a que cada
columna está formada en este caso por elementos todos distintos tenemos que este valor es
también máximo y L=1; ahora bien, el estado 2 es el único que cumple con
tener valores de R=3 y L=1 para generar un 0, por lo tanto M=1,
al final tenemos que 
cumpliendo con la propiedad
de los índices de Welch, si hacemos extensivo este estudio para las demás matrices de
conectividad obtenemos los mismos resultados, satisfaciendo de esta manera la condición
de combinabilidad.
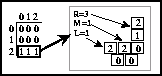
Figura: Matriz de conectividad del estado 0 del ACLR(3,h) regla
715 y como se manifiesta los índices de Welch en ésta.
Este comportamiento se observa claramente en el diagrama de subconjuntos asociado al ACLR(3,h); partiendo desde el estado 2 se puede llegar con un 0 a todos los nodos posibles del diagrama de de Bruijn, así en el diagrama de subconjuntos existe una liga que va desde el subconjunto unitario 4 al subconjunto completo 7 (R=3) mientras que con la regla de evolución reflejada la direccioón de las ligas en su diagrama de subconjuntos simboliza la evolución desde donde termina la vecindad hasta donde inicia en la regla original, con lo que tenemos que para generar un 0 terminando en el estado 2 solo existe una extensión compatible izquierda que es otro estado 2 , o lo que eslo mismo un ciclo de longitud 1 en el diagrama de subconjuntos en el nodo 4 (L=1), como desde el nodo 4 (estado 2) en ambos diagramas de subconjuntos es el único donde podemos extendernos por la derecha o izquierda para generar 0, tenemos que M=1 y se cumple que LMR=3.
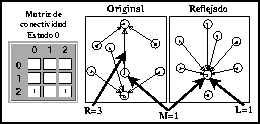
Figura: Diagramas de subconjuntos y valores de L, M y R
para la matriz de conectividad del estado 0 del ACLR(3,h) regla 715.
Este comportamiento se puede observar para los demás estados en los diagramas de subconjuntos tanto de la regla original como de la regla reflejada.
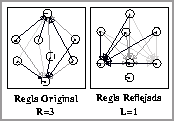
Figura: Diagramas de subconjuntos (regla original y reflejada) del
ACLR(3,h) regla 715.
Sin embargo, al checar solo las matrices de conectividad de un ACL solo estamos estudiando las rutas de longitud 1 ó lo que es lo mismo los ancestros de las cadenas de un elemento; pero hemos visto que la propiedad de combinabilidad no necesariamente tiene que presentarse en las cadenas de longitud 1 sino que puede aparecer hasta cadenas que tengan un mayor número de estados, entonces cómo podemos utilizar las matrices de conectividad para estudiar cadenas de longitud mayor que 1 ó equivalentemente, rutas de longitud mayor que 1 en el diagrama de de Bruijn.
Es bien conocido en la Teoría de Gráficas que si una matriz de conectividad se eleva a cierta potencia estará representando las rutas que existen en la gráfica asociado con longitud igual a esa potencia, así ésto se puede extender más ya que la multiplicación de dos matrices de conectividad de una gráfica representa las rutas que existen en el mismo formadas por los arcos cuyos valores corresponden a los de las matrices de conectividad.
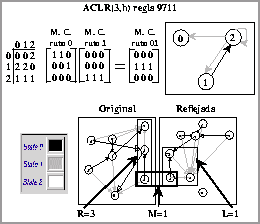
Figura: Indices de Welch para la cadena 01 del ACLR(3,h) regla
9711.
En la figura observamos las matrices de conectividad de los estados 0 y 1, en el caso de la matriz del estado 0 por si sola no tiene el valor necesario de los índices de Welch para considerarla como reversible, pero al multiplicarla por la matriz del estado 1 para obtener la matriz de conectividad de la cadena 01, se observa en el resultado que el valor de los índices satisface la propiedad de combinabilidad; si extendemos este análisis para todas las matrices de conectividad de las cadenas de longitud 2 y este comportamiento se presenta en todos los casos, se satisface por completo la propiedad de combinabilidad y el ACL es reversible, en caso contrario, se tendrán que checar las matrices de conectividad de las cadenas de longitud 3 y así sucesivamente.
En síntesis, para leer el valor de los índices de Welch desde una matriz de
conectividad y saber si está cumpliendo con el principio de combinabilidad el número de
elementos diferentes a 0 por cada renglón debe ser igual a 0 ó R,
el número de elementos diferentes de 0 por cada columna debe ser igual a 0
ó L y la suma de elementos en la diagonal principal debe ser 1, es decir,
un solo ciclo es permitido para producir la secuencia de estados representada por la
matriz de conectividad; si cada matriz de conectividad correspondiente a cada cadena
posible de una longitud dada (que puede ser mayor o igual a 2r) cumple estas
características y con 
se concluye que para cada
una de estas cadenas el valor de M=1 y por lo tanto el ACL es reversible.
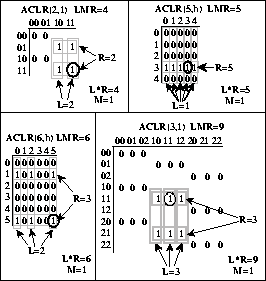
Figura: Diferentes formas de matrices de conectividad para ACLR, con un
solo 1 en la diagonal principal y valores de 
induciendo que M=1.
Para un ACL no reversible el proceso anterior generará matrices de conectividad en
donde ya sea que la suma de los elementos de la matriz sea diferente a 
y por lo tanto no se cumpla la multiplicidad uniforme ó la suma de
elementos en la diagonal principal sea mayor que 1 con lo que existirían multiples
ancestros para una cadena dada.
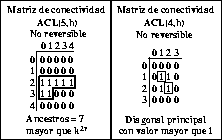
Figura: Matrices de conectividad para ACL no reversibles.