![]()
A continuación se presentará un proceso el cual utiliza las propiedades anteriormente expuestas para calcular todos las posibles reglas reversibles para un ACL(k,r), como forma de ejemplificar lo anterior se tomará el caso de un ACL(4,h) pero este proceso se puede adaptar para cualquier caso; la estrategia a seguir es ir generando todas las matrices de evolución posibles que cumplan las propiedades por estados individuales necesarias para que el ACL sea reversible, para ésto se tomará una plantilla para la matriz de evolución donde los elementos de la diagonal principal sean diferentes entre sí y permanezcan sin cambio durante el proceso.
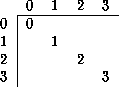
Tabla: Plantilla para generar todas las matrices de evolución posibles
candidatas a ser ACLR(4,h).
Sobre esta plantilla se empezará a colocar los elementos de cada estado desde 0 a k-1 (en el ejemplo anterior de 0 a 3), cumpliendo con que cada estado debe aparecer el mismo número de veces que los demás.
Un proceso adicional en el método es verificar conforme se actualiza cada estado que no se formen dos o más ciclos iguales de longitud 2 con nodos distintos (cosa que no puede ocurrir en un ACLR pues indica que una secuencia de dos elementos puede ser generada por varias cadenas de dos elementos); la forma de verificar ésto es formar una matriz auxiliar en donde cada renglón representará un estado del ACL y los elementos del mismo una codificación de las vecindades que lo generan, esto puede ser elevar al cubo el valor de cada célula que pertenece al ancestro del estado y sumar los valores.
Si existen dos valores iguales en un renglón significa que existe un ciclo de longitud 2 formado por un mismo estado, de este modo una secuencia de cualquier longitud formada por este estado tendría dos ancestros posibles uno compuesto por los elementos del ciclo y otro por las coordenadas de la diagonal principal donde se localiza el estado.
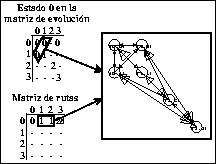
Figura: Matriz de rutas del estado 0 en un ACL(4,h) donde se
observan múltiples ancestros.
Si un renglón tiene dos valores que aparecen en otro renglón significa que existen dos ciclos iguales de longitud 2 formado por distintos nodos, así una secuancia formada por los elementos del ciclo tiene como posibles ancestros cadenas compuestas ya sea por los nodos de uno de los ciclos ó por los nodos del otro, evitando que sea reversible.
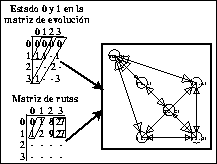
Figura: Matriz de rutas del estado 0 y 1 en un ACL(4,h)
donde se observan múltiples ancestros.
Aunque este paso no es necesario para detectar ACLR es de gran utilidad ya que nos ayudará a descartar muchas matrices de evolución de manera rápida y por lo tanto agilizar el proceso de cálculo.
Una vez que la matriz se ha llenado la matriz de evolución completamente con los elementos de cada estado, se procede a verificar si las matrices de conectividad para cadenas de un elemento cumplen con el principio de combinabilidad de Nasu, de no ser así se verifican las matrices de conectividad de cadenas de dos elementos y se continúa de esta forma ya sea hasta que todas las matrices de conectividad generadas cumplan con ser debilmente combinables (y por lo tanto el ACL es reversible) obteniendo el cluster mínimo del mismo para guardarlo, o que se cumpla en cualquier matriz de conectividad alguna de las condiciones presentadas para descartar la regla de evolución como reversible.
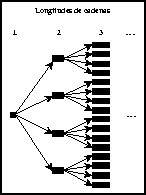
Figura: Crecimiento del número de matrices de conectividad a revisar
para cadenas de longitud 1 en adelante para un ACL(4,h).
El proceso completo se realiza para toda matriz de evolución genarada; se empezará a
llenar la plantilla de la matriz de evolución con el estado n para ![]() ; en síntesis el algoritmo sería de la siguiente
forma:
; en síntesis el algoritmo sería de la siguiente
forma:
El siguiente diagrama refleja el flujo del programa; el listado del mismo para el caso (4,h) se presenta en el Apéndice A.
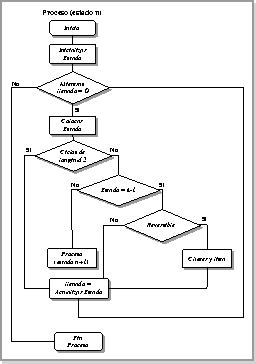
Figura: Flujo del proceso para obtener ACLR(k,r).
![]()