Posterior: Elementos con orden arbitrario Arriba: Algoritmo cuántico para el Anterior: Algoritmo cuántico para el

Elementos con orden potencia de 2

Supongamos dado $m\in\Phi(n)$ y que éste es tal que su orden $r$ es una potencia de 2.

Sea $P_1=H^{\otimes \kappa}\otimes I^{\otimes \nu}$ donde $H,I:\mathbb{H}_1\to\mathbb{H}_1$ son los operadores de Hadamard e identidad respectivamente. Por la ec. (4) se tiene $P_1(\mbox{\bf e}_{\mbox{\scriptsize\bf0}}\otimes \mbox{\bf e}_{\mbox{\scriptsiz... ...scriptsize\boldmath$\varepsilon$}}\otimes \mbox{\bf e}_{\mbox{\scriptsize\bf0}}$. Escribamos $\mbox{\bf s}_1=P_1(\mbox{\bf e}_{\mbox{\scriptsize\bf0}}\otimes \mbox{\bf e}_{\mbox{\scriptsize\bf0}})$. Ahora, aplicando el operador $V_m$, resulta $V_m(\mbox{\bf s}_1) = \frac{1}{\sqrt{2}^{\kappa}}\sum_{i=0}^{2^{\kappa}-1} \mbo... ...$}_i}\otimes \mbox{\bf e}_{\mbox{\scriptsize\boldmath$\varepsilon$}_{f(i,0,m)}}$. Escribamos $\mbox{\bf s}_2=V_m(\mbox{\bf s}_1)$.

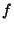Ya que $f(i,0,m)=m^i\,\mbox{mod}\,n$, $f$ es una función periódica de período $r$ respecto a $i$. Sea $J_j =\{i\vert\leq i\leq 2^{\kappa}-1: \, i=j\,\mbox{mod}\,r\}$ la clase de índices que dejan residuo $j$ al dividírseles entre $r$. Claramente $[\![0,2^{\kappa}-1]\!] = \bigcup_{j=0}^{r-1} J_j$, y la cardinalidad de cada conjunto $J_j$ es $s=\frac{2^{\kappa}}{r}$, el cual número, para este caso, es entero. Por tanto, es posible reescribir

$$\mbox{\bf s}_2= \frac{1}{\sqrt{2}^{\kappa}}\sum_{j=0}^{r-1}\... ...\mbox{\bf e}_{\mbox{\scriptsize\boldmath$\varepsilon$}_{m^j}}.$$ (12)

Si aquí se aplica el postulado de medición, entonces se elegirá a un vector de la forma $\mbox{\bf e}_{\mbox{\scriptsize\boldmath$\varepsilon$}_i}\otimes \mbox{\bf e}_{\mbox{\scriptsize\boldmath$\varepsilon$}_{m^{j_0}}}$, $i\in J_{j_0}$, para una potencia fija $j_0\leq r$, con probabilidad $\frac{r}{2^{\kappa}}$. El estado correspondiente a esta situación es de la forma

$$\mbox{\bf s}_3= \sum_{i=0}^{2^{\kappa}-1} g(i)\mbox{\bf e}_{... ...x{\bf e}_{\mbox{\scriptsize\boldmath$\varepsilon$}_{m^{j_0}}}.$$ (13)

donde $g:i \mapsto \left\{\begin{array}{cl} \sqrt{\frac{r}{2^{\kappa}}} & \mbox{ si }i \in J_{j_0} \\ 0 & \mbox{ si }i\not\in J_{j_0} %%\\ \end{array}\right.$

La función $g$ también es periódica, de período $r$. Ahora, se tiene que la transformada de Fourier de $g$, $\hat{g}$ será también periódica pero de período proporcional a $\frac{1}{r}$.

Calculemos la transformada inversa discreta de Fourier de $\mbox{\bf s}_3$:

$$\check{\mbox{\bf s}_3} = \mbox{TDF}^H(\mbox{\bf s}_3) = \sqrt... ...{\bf e}_{\mbox{\scriptsize\boldmath $\varepsilon$}_{m^{j_0}}},$$

y al intercambiar el orden de las sumatorias se obtiene:

$$\mbox{\bf s}_4 = \check{\mbox{\bf s}_3} = \frac{1}{\sqrt{r}}... ...x{\bf e}_{\mbox{\scriptsize\boldmath$\varepsilon$}_{m^{j_0}}}.$$ (14)

Ya que $\mbox{exp}\left(-\frac{2\pi i \ell}{s}\right)$ es una raíz $s$-ésima de la unidad, se tiene $\frac{1}{s} \sum_{k=0}^{s-1} \mbox{exp}\left(-\frac{2\pi i \ell k}{s}\right)$ será 1 o 0 en función de que $\ell$ sea o no un múltiplo entero de $s$, es decir un número de la forma $\ell = ts$, con $t=0,\ldots,r-1$. Aquí es esencial el hecho de que $s$ es entero. Así pues, de (14),

$$\mbox{\bf s}_4 = \frac{1}{\sqrt{r}}\left(\sum_{t=0}^{r-1} \m... ...x{\bf e}_{\mbox{\scriptsize\boldmath$\varepsilon$}_{m^{j_0}}}.$$ (15)

Las relaciones (13) y (15), que expresan a $\mbox{\bf s}_3$ y $\mbox{\bf s}_4 = \check{\mbox{\bf s}_3}$, involucran ambas al orden $r$. Pero hay una diferencia esencial entre ellas: En (13) los índices $i$, en el primer qubit, correspondientes a coeficientes no-nulos dependen de la potencia ``aleatoria'' $j_0$, en tanto que en (15) no dependen de ésa, e involucran sin embargo, a $r$.

Si ahora se aplica el postulado de medición se obtendrá un valor de la forma $\frac{2^{\kappa}t_0}{r}$, con $t_0\in[\![0,r-1]\!]$, cada uno con probabilidad $r^{-1}$. Si $t_0=0$, entonces no es posible obtener ninguna información acerca de $r$ y se ha de repetir el procedimiento otra vez. En otro caso, al dividir entre $2^{\kappa}$ se tiene el valor racional $\frac{r_0}{r_1}=\frac{t_0}{r}$. Se conoce a $r_0$ y $r_1$ mas aún no se conoce $t_0$ ni $r$. Sin embargo, necesariamente $r_1$ divide a $r$. Así pues, se puede aplicar de nuevo el algoritmo cuántico a partir de $m_1=m^{r_1}$. Procediendo recursivamente se obtiene una factorización $r=r_1r_2\cdots r_{p}$ conteniendo a lo más $\log_2 r$ factores.

En resumen, el algoritmo para localizar divisores de órdenes de elementos es el siguiente:

Entrada.

$n\in\mathbb{N}$, $m\in\Phi(n)$ de orden potencia de 2.

Salida.

$r$ tal que $r\vert o(m)$.

Procedimiento

DivisorOrdenPotencia2$(n,m)$

1. Sea $\nu:=\lceil \log_2 n\rceil$, $\kappa:=2\nu$.
2. Defínase $V_m:\mathbb{H}_{\kappa+\nu}\to \mathbb{H}_{\kappa+\nu}$ como en la ec. (11).
3. Sea $\mbox{\bf s}_1:=(H^{\otimes \kappa}\otimes I^{\otimes \nu})(\mbox{\bf e}_{\mbox{\scriptsize\bf0}}\otimes \mbox{\bf e}_{\mbox{\scriptsize\bf0}})$.
4. Sea $\mbox{\bf s}_2 := V_m(\mbox{\bf s}_1)$.
5. Sea $\mbox{\bf s}_3 := \sum_{i=0}^{2^{\kappa}-1} g(i)\mbox{\bf e}_{\mbox{\scriptsize... ...}_{i}}\otimes \mbox{\bf e}_{\mbox{\scriptsize\boldmath$\varepsilon$}_{m^{j_0}}}$ el estado equivalente a ``tomar una medición'' en $\mbox{\bf s}_2$. Entonces $g$ queda determinada como en la ec. (13).
6. Sea $\mbox{\bf s}_4 := \mbox{\tt TIDF}(2^{\kappa},\mbox{\bf s}_3)$ la transformada inversa discreta de Fourier de $\mbox{\bf s}_3$.
7. Sea $\mbox{\bf e}_{\mbox{\scriptsize\boldmath$\varepsilon$}_{k}}\otimes \mbox{\bf e}_{\mbox{\scriptsize\boldmath$\varepsilon$}_{m^{j_0}}}$ una medición de $\mbox{\bf s}_4$.
8. Si $k==0$ repítase desde el paso 3. En otro caso sea $\frac{r_0}{r_1}=\frac{k}{2^{\kappa}}$ y dése como resultado $r_1$.

El algoritmo para calcular órdenes de elementos es el siguiente:

Entrada.

$n\in\mathbb{N}$, $m\in\Phi(n)$ de orden potencia de 2.

Salida.

$r$ tal que $r=o(m)$.

Procedimiento

OrdenPotencia2$(n,m)$

1. Sean inicialmente $r:=1$ y $m_1:=m$.
2. Repítase
   1. sea $r_1:=\mbox{\tt DivisorOrdenPotencia2}(n,m_1)$;
   2. actualícese $r:=r\cdot r_1$;
   3. actualícese $m_1:=m_1^{r_1}\mbox{ mod }n$.
   hasta tener $r_1==1$.
3. Dése como resultado $r$.

Posterior: Elementos con orden arbitrario Arriba: Algoritmo cuántico para el Anterior: Algoritmo cuántico para el