Diagramas de de Bruijn

Históricamente los diagramas de de Bruijn fueron creados para representar y analizar el problema de tener un registro de corrimientos de las distintas secuencias de un conjunto de símbolos dado. Esta idea puede ser aplicada en autómatas celulares para el estudio de períodos, cuestionandose que secuencias de células pueden aparecer con evoluciones periódicas.

Los nodos del diagrama de de Bruijn son secuencias de tamaño $2r$ de símbolos de $K$, las ligas dirigidas del diagrama describen como tales secuencias pueden traslapar donde los $2r-1$ símbolos finales del nodo inicial deben concordar con $2r-1$ símbolos iniciales del nodo final. De este modo, cada liga representa una vecindad completa del autómata. La matriz de incidencia del diagrama de de Bruijn se representa como:

$$M_{i,j} = \left\{\begin{array}{lllll} 1&si&j&=& \left\{\begin{arr... ... \end{array} \right.\ \\ \\ 0& \mbox{en otro caso} \\ \end{array} \right.$$

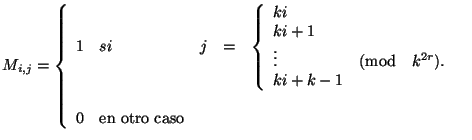
A través del diagrama de de Bruijn se pueden representar configuraciones o clases de configuraciones en un autómata celular, el etiquetado de cada liga se asocia con la vecindad que representa y su evolución especificada por la regla $\varphi$.

En estos términos deben existir $k$ ligas de entrada en cada nodo y $k$ ligas de salida en cada nodo, en total se tienen $k^{2r}$ nodos unidos con $k^{2r+1}$ ligas, correspondiendo a el total de vecindades. El diagrama de de Bruijn es totalmente regular aunque es asimétrico; el diagrama de de Bruijn para la regla 110 se muestra en la Figura 1.

Figura 1: Diagrama de de Bruijn para la regla 110