




Siguiente: Mapas compatibles en cada
Arriba: Producto de variedades
Anterior: Producto de variedades
Sean  ,
,  espacios topológicos. Consideramos el producto topológico
espacios topológicos. Consideramos el producto topológico
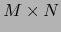 y las proyecciones canónicas:
y las proyecciones canónicas:
definidas por:
Se sabe de topología general que dichas proyecciones canónicas son aplicaciones
continuas.
Supongamos que existen mapas
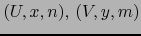 de sendos espacios topológicos
de sendos espacios topológicos  ,
,  .
Designemos por
.
Designemos por 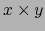 la aplicación del abierto
la aplicación del abierto  de
de 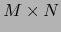 en el abierto
en el abierto
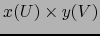 de
de
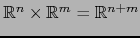 dada por:
dada por:
Sin los argumentos  esta fórmula se escribe equivalentemente:
esta fórmula se escribe equivalentemente:
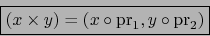 |
(4) |
Para todo par
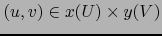 existe un único par
existe un único par
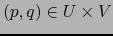 tal que:
tal que:
a saber
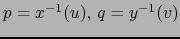 . Luego la aplicación
. Luego la aplicación 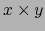 es una biyección de
es una biyección de  sobre
sobre
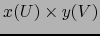 .
.
Afirmamos que 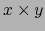 es una aplicación continua. De topología general
sabemos que para ello basta probar que son continuas las aplicaciones:
es una aplicación continua. De topología general
sabemos que para ello basta probar que son continuas las aplicaciones:
Pero esto es cierto, pues, la aplicación (5) no es otra que
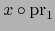 y
la aplicación (6) no es otra que
y
la aplicación (6) no es otra que
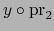 .
.
Análogamente, usando las proyecciones canónicas:
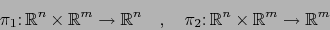 |
(7) |
vemos que la aplicación
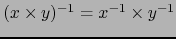 de
de
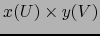 en
en 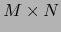 es continua.
Viene, pues, probado que la aplicación
es continua.
Viene, pues, probado que la aplicación 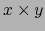 es un homeomorfismo del
abierto
es un homeomorfismo del
abierto  de
de 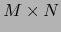 sobre el abierto
sobre el abierto
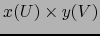 de
de
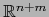 ,
o sea:
,
o sea:
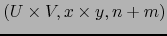 es un mapa del espacio topológico
es un mapa del espacio topológico 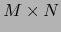
.
De lo dicho resulta sin más:
El producto topológico de dos variedades topológicas es una variedad topológica.
Precisamente hablando: si 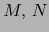 son variedades topológicas provistas de
sendos atlas
son variedades topológicas provistas de
sendos atlas
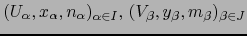 ,
la familia
,
la familia
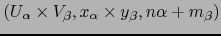 es un atlas
de
es un atlas
de 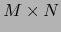 .
.
En particular si M, N son variedades topológicas puras, también 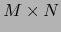 es una variedad topológica pura y vale:
es una variedad topológica pura y vale:





Siguiente: Mapas compatibles en cada
Arriba: Producto de variedades
Anterior: Producto de variedades
Guillermo M. Luna
2009-06-14
![]() es una aplicación continua. De topología general
sabemos que para ello basta probar que son continuas las aplicaciones:
es una aplicación continua. De topología general
sabemos que para ello basta probar que son continuas las aplicaciones:
![% latex2html id marker 57252
\fbox{\begin{minipage}{12cm} Las coordenadas relat...
...x{\rm pr}_2 \quad \forall\, j \in [\![ 1,m ]\!] \end{displaymath}\end{minipage}}](img4135.png)
![]() son variedades topológicas provistas de
sendos atlas
son variedades topológicas provistas de
sendos atlas
![]() ,
la familia
,
la familia
![]() es un atlas
de
es un atlas
de ![]() .
.
![]() es una variedad topológica pura y vale:
es una variedad topológica pura y vale: