




Siguiente: Aplicaciones diferenciables
Arriba: Producto de variedades
Anterior: Un mapa en cada
Consideremos ahora dos mapas
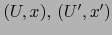 compatibles
compatibles
 sobre
sobre  y dos mapas
y dos mapas
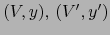 compatibles
compatibles  sobre
sobre  .
Supondremos
.
Supondremos
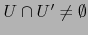 y
y
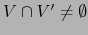 ,
equivalentemente:
,
equivalentemente:
Nos fijamos en los cambios de mapas:
Ponemos:
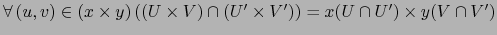 tenemos:
tenemos:
o sea, usando las proyecciones canónicas
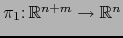 y
y
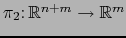 :
:
Por hipótesis, las aplicaciones
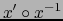 e
e
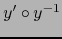 son
de clase
son
de clase  . Luego, en virtud del teorema 4.5.2, las funciones
. Luego, en virtud del teorema 4.5.2, las funciones
 son de clase
son de clase
 . Ya que
. Ya que 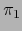 y
y 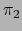 son de clase
son de clase  , el teorema 4.5.5 implica que
todas las funciones
, el teorema 4.5.5 implica que
todas las funciones
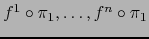 ;
;
 son
de clase
son
de clase  . Usando de nuevo el teorema 4.5.2, vemos por (8) que el cambio de mapa
. Usando de nuevo el teorema 4.5.2, vemos por (8) que el cambio de mapa
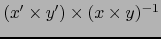 es de clase
es de clase  , o sea, los mapas
, o sea, los mapas
 y
y
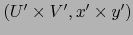 son compatibles
son compatibles  .
.
Así pues, si
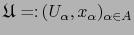 y
y
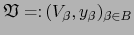 son atlas coherentes
son atlas coherentes  sobre sendos espacios M, N, el atlas:
sobre sendos espacios M, N, el atlas:
es un atlas coherente  sobre
sobre 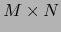 .
.
Supongamos finalmente que  y
y  son dos variedades
son dos variedades  . Sean
. Sean
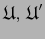 dos atlas admisibles sobre
dos atlas admisibles sobre  y
y
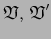 dos atlas
admisibles sobre
dos atlas
admisibles sobre  . Entonces los atlas
. Entonces los atlas
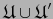 y
y
 son coherentes
son coherentes  , luego, por lo
que se acaba de ver
, luego, por lo
que se acaba de ver
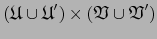 es un atlas coherente
es un atlas coherente  sobre
sobre 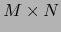 . Pero el atlas
. Pero el atlas
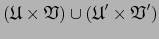 está contenido en este último, luego es también coherente
está contenido en este último, luego es también coherente  , o sea:
, o sea:
La clase de equivalencia del atlas
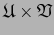 sobre
sobre
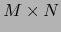 es independiente de la elección de los atlas admisibles
es independiente de la elección de los atlas admisibles 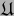 ,
, 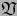 de sendas variedades
de sendas variedades  ,
,  . Dicha clase de equivalencia define sobre el espacio
. Dicha clase de equivalencia define sobre el espacio
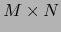 la estructura de una variedad
la estructura de una variedad  llamada el PRODUCTO DE LAS VARIEDADES
llamada el PRODUCTO DE LAS VARIEDADES  ,
,  de clase
de clase  .
.
Informalmente se habla simplemente de la VARIEDAD PRODUCTO  .
Si
.
Si  y
y  son variedades puras, vale:
son variedades puras, vale:





Siguiente: Aplicaciones diferenciables
Arriba: Producto de variedades
Anterior: Un mapa en cada
Guillermo M. Luna
2009-06-14
![]() compatibles
compatibles
![]() sobre
sobre ![]() y dos mapas
y dos mapas
![]() compatibles
compatibles ![]() sobre
sobre ![]() .
Supondremos
.
Supondremos
![]() y
y
![]() ,
equivalentemente:
,
equivalentemente:
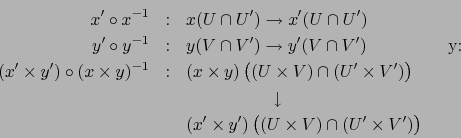
![\begin{eqnarray*}
x^\prime \circ x^{-1} &=& (f^1,\ldots,f^n) \quad \mbox{con} \q...
...e) \to {{\mathbb{R}}} \hspace{3em} \forall\, j \in [\![ 1,m ]\!]
\end{eqnarray*}](img4145.png)
![]() y
y
![]() son atlas coherentes
son atlas coherentes ![]() sobre sendos espacios M, N, el atlas:
sobre sendos espacios M, N, el atlas:
![]() y
y ![]() son dos variedades
son dos variedades ![]() . Sean
. Sean
![]() dos atlas admisibles sobre
dos atlas admisibles sobre ![]() y
y
![]() dos atlas
admisibles sobre
dos atlas
admisibles sobre ![]() . Entonces los atlas
. Entonces los atlas
![]() y
y
![]() son coherentes
son coherentes ![]() , luego, por lo
que se acaba de ver
, luego, por lo
que se acaba de ver
![]() es un atlas coherente
es un atlas coherente ![]() sobre
sobre ![]() . Pero el atlas
. Pero el atlas
![]() está contenido en este último, luego es también coherente
está contenido en este último, luego es también coherente ![]() , o sea:
, o sea:
![]() .
Si
.
Si ![]() y
y ![]() son variedades puras, vale:
son variedades puras, vale: