



Siguiente: About this document ...
Arriba: FUNDAMENTOS DE VARIEDADES DIFERENCIABLES
Anterior: Bibliography
- álgebra
- álgebra alternada sobre el subespacio

- álgebra asociativa
- álgebra conmutativa
- álgebra de Grassman sobre
 asociada con la base
asociada con la base
- álgebra exterior dual sobre
- álgebra exterior sobre el espacio vectorial

- álgebra unífera
- álgebras de Lie
- área del paralelogramo
- órbita trivial
- órbitas
- (Fórmula de incrementos finitos)
- (regla de la cadena para semiespacios cerrados)
- (Regla de la cadena)
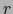 -vector
-vector 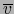 divide al
divide al 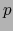 -vector
-vector 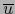
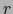 -covectores
-covectores
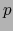 -vector
-vector
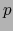 -vector descomponible
-vector descomponible
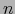 -vector patrón sobre
-vector patrón sobre
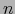 -covector patrón
-covector patrón
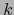 veces continuamente diferenciable en el abierto
veces continuamente diferenciable en el abierto
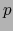 -vectores
-vectores
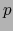 -vectores descomponibles
-vectores descomponibles
- abierto de primera especie
- abierto de segunda especie
- ajena
- altura del paralelotopo
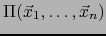 relativa
relativa
- ampliación exterior de la aplicación lineal
- anulador del conjunto
- aplicación afín
- aplicación bilineal
- aplicación continuamente diferenciable en el abierto
- aplicación de clase
,
![[*]](crossref.png)
- aplicación de clase
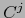
- aplicación dual
- aplicación lineal alternante
- aplicación lineal antisimétrica
- aplicación lineal simétrica
- aplicación quieta (en el abierto
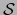 )
)
- aplicación quieta
![[*]](footnote.png) en el punto
en el punto
- aplicación
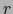 -lineal
-lineal
- aplicación
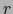 -lineal alternada
-lineal alternada
- aplicación
 es diferenciable en el punto
es diferenciable en el punto
- aplicaciones parciales
,
![[*]](crossref.png)
- apunta hacia el semiespacio
- atlas
,
![[*]](crossref.png)
- atlas admisible
,
![[*]](crossref.png) ,
, ![[*]](crossref.png)
- atlas coherente
- atlas coherente
 maximal
maximal
- atlas
 equivalentes
equivalentes
- Ausdehnungslehre
- automorfismos afines
- axioma de Borel-Lebesgue
- axioma de Hausdorff
- base calibrada
- base de
dicho espacio inducida por el mapa admisible
- base de sentido positivo
- base de
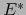 dual de la base
dual de la base
- base de
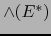 asociada con la base
asociada con la base
- base de
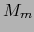 inducida por el mapa admisible
inducida por el mapa admisible
- base del subespacio
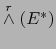 asociada
asociada
- base O.N.
- base O.N.P.
- base ortogonal
- base ortonormal
- bidual de un espacio vectorial
- bivector
- borde de
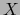
- Bourbaki
- cambio de mapa
- cambios de mapas
- Carácter local de la diferencial
- ciclo
- clase
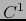 en el abierto
en el abierto
- clase

- clase
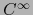
- clase
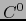
- clase
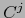
- Claude Chevalley
- cofactor del elemento
- coherente
- columna número
- compañera de la desigualdad del triángulo
- compatibles
,
![[*]](crossref.png)
- componentes contravariantes del covector
- componentes contravariantes del vector
- componentes covariantes del covector
- componentes covariantes del vector
- conjunto convexo
- coordenadas del punto
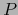 con respecto al referencial
con respecto al referencial
- coordenadas locales
- coordenadas relativas al mapa
- covectores
- curva
- curva en el semiplano cerrado
- dígitos
- de segunda especie
- Delta de Kronecker Generalizada
- derivada de la aplicación
 en el punto
en el punto 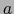 según el vector
según el vector 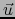
- derivada parcial
- derivada parcial de
 en
en 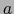 , de índice
, de índice 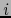 con respecto a la base
con respecto a la base
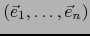
- derivada parcial de
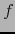 con respecto al mapa admisible
con respecto al mapa admisible
- derivadas parciales de orden
- desarrollo
- desarrollo del determinante
- determinante de Gram
- determinante de la matriz
- determinante del endomorfismo
- determinante del
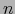 -uplo
-uplo
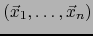 de vectores
de vectores
- diferenciable
- diferenciable en el punto
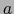
- diferenciable en un punto
,
![[*]](crossref.png)
- diferencial de la aplicación
 en el punto
en el punto 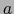
- diferencial de la aplicación
 en el punto
en el punto 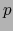
- diferencial de la aplicación
 en el punto
en el punto 
- diferencial de la aplicación
 en el punto
en el punto  de la variedad con borde
de la variedad con borde 
- diferenciales parciales de la aplicación
 en el punto
en el punto 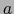
- dimensión de la variedad
,
![[*]](crossref.png)
- dimensión de la variedad afín
- dimensión infinita
- dimensión
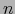
- dirección
- dirección de la variedad afín
- divisible
- dominio del mapa
- dual topológico
- elemento homogéneo
- elemento homogéneo de grado
- elementos homogéneos de grado
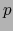
- elementos simples
- Elie Cartan
- en el tiempo
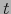
- equivalentes
- escalares
- espacio afín normado
- espacio afín sobre el espacio vectorial
,
![[*]](crossref.png)
- espacio casi compacto
- espacio compacto
- espacio de Banach
- espacio de base numerable
- espacio de producto escalar
- espacio dual
- espacio localmente compacto
- espacio proyectivo
- espacio separado
- espacio vectorial asociado con el espacio afín
- espacio vectorial euclidiano
- espacio vectorial normado
- espacio vectorial orientado
- espacio vectorial tangente
- espacio vectorial tangente a la variedad con borde
 en el punto
en el punto 
- espacio vectorial tangente a la variedad en el punto
- espacio vectorial tangente al semiespacio cerrado
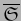 en el punto
en el punto 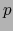
- espacio vectorial (real) orientado
- estructura canónica de espacio vectorial euclidiano
- estructura de espacio de producto escalar inducida
- estructura de espacio de producto escalar sobre
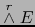 inducida
inducida
- estructura de producto escalar sobre
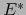 inducida por la de
inducida por la de 
- estructura de variedad diferenciable inducida sobre el borde
- estructura de variedad
 inducida sobre el abierto
inducida sobre el abierto
- estructura natural
- estructura natural de variedad
- estructura natural de variedad con borde
- estructura natural de variedad diferencial
,
![[*]](crossref.png)
- estructura
 sobre
sobre  inducida por el homomorfismo
inducida por el homomorfismo
- fórmula de cambio de coordenadas
- fórmula de Cauchy-Binet
- fórmula de Cauchy-Binet para productos vectoriales
- fórmula de Cauchy-Binet para productos vectoriales en dimensión
- fórmula del ascenso del índice
- fórmula del descenso del índice
- fórmula del doble producto vectorial
- fórmula del producto vectorial reiterado
- familia ortogonal
- familia ortonormal
- fila número
- forma lineal
- forma
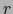 -lineal alternada
-lineal alternada
- formas exteriores
- formas exteriores vectoriales de grado
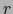 sobre el espacio vectorial
sobre el espacio vectorial  , de valores en
, de valores en 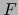
- función derivada parcial con respecto la
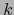 -ésima coordenada local
-ésima coordenada local
- función local en el punto

- función local en
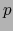 sobre
sobre
- funcional
- funcionales
- funciones coordenadas de
 con respecto al
referencial
con respecto al
referencial
- funciones locales
- funciones locales en el punto
- funciones locales en
 sobre
sobre 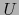
- G. Papy
- geometría afín
- gramiano
- grupo
- grupo afín
- grupo alternado de grado
- grupo lineal
- grupo simétrico de grado
- H. Flanders
- H. G. Ellis
,
![[*]](crossref.png)
- Hermann Grassmann
- hiperplano
- homeomorfismo local
- homomorfismo
- homotecia de razón
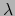
- identidad de Jacobi
- identidad de Lagrange
- imagen de la curva
- inmersión en el punto
- inmersión (en el abierto
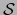 )
)
- invariancia de la dimensión
- invariancia del recinto
- inversiones de la permutación
- inversiones del par
- isometría
- isometría lineal
- isomorfa
- isomorfismo
- isomorfismo afín de
 sobre
sobre 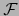
- isomorfismo diferenciable
- isomorfismo

- isomorfismo
 de
de 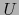 sobre
sobre 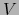
- isomorfismo
 de la variedad diferenciable
de la variedad diferenciable  sobre la variedad diferenciable
sobre la variedad diferenciable 
- J. Dieudonné
,
![[*]](crossref.png)
- J. Dixmier
- jacobiano de la aplicación
- L. Schwartz
- leída en los mapas
- ley del producto mixto
- Liutzen E. J. Brouwer
- localización de vectores tangentes
- magnitud
- mapa
- mapa admisible
,
![[*]](crossref.png) ,
, ![[*]](crossref.png)
- mapa admisible de la variedad con borde
- mapa de dimensión
- mapa de primera especie
- mapa en el punto
- mapas afines
- matriz de transición de la antigua base
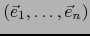 de
de  a la nueva base
a la nueva base
- matriz jacobiana de la aplicación
- matriz transpuesta de la matriz
- menores de orden
- multiplicación
- multiplicación exterior
- multiplicación exterior con respecto a la aplicación bilineal
- no degenerada
- norma
- norma euclidiana
- norma sobre
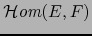 inducida por las normas
inducida por las normas
- normas equivalentes
![[*]](crossref.png)
![[*]](footnote.png) en el punto
en el punto
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png) ,
, ![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png) ,
, ![[*]](crossref.png)
![[*]](crossref.png)
![[*]](footnote.png) en el punto
en el punto
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png) ,
, ![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png) ,
, ![[*]](crossref.png)