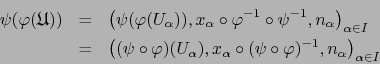Siguiente: Producto de variedades
Arriba: Mapas y atlas admisibles.
Anterior: Estructura inducida por un
Definición 1.9
Sean 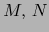 variedades
variedades  y
y  un homeomorfismo del espacio topológico
un homeomorfismo del espacio topológico
 sobre el espacio topológico
sobre el espacio topológico  .
.  se dice ISOMORFISMO DE LA VARIEDAD DIFERENCIABLE SOBRE LA VARIEDAD DIFERENCIABLE si la estructura
se dice ISOMORFISMO DE LA VARIEDAD DIFERENCIABLE SOBRE LA VARIEDAD DIFERENCIABLE si la estructura  inducida
por el homeomorfismo
inducida
por el homeomorfismo  sobre N coincide con la estructura
sobre N coincide con la estructura  dada sobre
dada sobre  .
.
Equivalentemente:
Para cierto atlas admisible 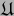 sobre
sobre  ,
,
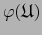 es un
atlas admisible de
es un
atlas admisible de  . (En tal caso, lo mismo ocurre para cualquier atlas admisible
. (En tal caso, lo mismo ocurre para cualquier atlas admisible
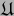 sobre
sobre  .)
.)
Aquí, como en el capítulo 4, no usaremos la mal ensamblada palabra
``difeomorfismo'' como sustituto de ``isomorfismo  ''.
''.
Teorema 1.11
- Si
 es una variedad
es una variedad  , la aplicación idéntica
, la aplicación idéntica 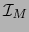 de
de
 es un isomorfismo
es un isomorfismo  de
de  sobre
sobre  .
.
- Si
 ,
,  son variedades
son variedades  y
y  es un isomorfismo
es un isomorfismo  de
de
 sobre
sobre  la aplicación
la aplicación 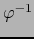 es un isomorfismo
es un isomorfismo  de
de  sobre
sobre  .
.
- Si
 ,
,  ,
, 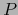 son variedades
son variedades  y además
y además  es un isomorfismo
es un isomorfismo
 de
de  sobre
sobre  y
y 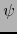 es un isomorfismo
es un isomorfismo  de
de  sobre
sobre 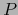 , la aplicación
, la aplicación
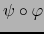 es un isomorfismo
es un isomorfismo  de
de  sobre
sobre 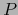 .
.
Demostración
Siendo evidentemente cierta la afirmación a., probemos b. y c.
- Sea
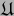 un atlas admisible de
un atlas admisible de  . Ya que por hipótesis,
. Ya que por hipótesis,  es un isomorfismo
es un isomorfismo  de
de  sobre
sobre  , el atlas
, el atlas
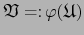 es un atlas admisible
sobre
es un atlas admisible
sobre  . Pero
. Pero
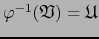 , atlas
admisible sobre
, atlas
admisible sobre  . Por lo tanto,
. Por lo tanto, 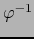 es un isomorfismo
es un isomorfismo  de
de 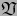 sobre
sobre 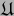 .
.
- Sea
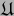 un atlas admisible de
un atlas admisible de  . Puesto que
. Puesto que  es un isomorfismo
es un isomorfismo
 de
de  sobre
sobre  , el atlas
, el atlas
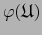 es un atlas
admisible de
es un atlas
admisible de  . Como
. Como 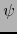 es un isomorfismo
es un isomorfismo  de
de  sobre
sobre 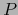 , el atlas
, el atlas
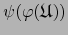 es un atlas admisible de
es un atlas admisible de 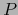 .
.
Si
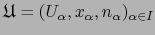 , se tiene
, se tiene
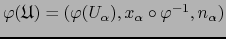 y
y
de donde
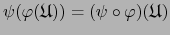 . La aplicación
. La aplicación
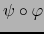 es, pues, un isomorfismo
es, pues, un isomorfismo  de
de  sobre
sobre 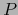 .
.

Definición 1.10
Sean  ,
,  variedades
variedades  . Se dice que la variedad
. Se dice que la variedad  es ISOMORFA
es ISOMORFA  a la variedad
a la variedad  , si existe un isomorfismo
, si existe un isomorfismo  de
de  sobre
sobre  .
.
El teorema 5.1.11 entraña sin más:
Teorema 1.12
- Toda variedad diferenciable
 de clase
de clase  es isomorfa
es isomorfa  a sí misma.
a sí misma.
- Si
 ,
,  son variedades
son variedades  y
y  es isomorfa
es isomorfa  a
a  , la variedad
, la variedad
 es isomorfa
es isomorfa  a
a  .
.
- Si
 ,
,  ,
, 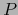 son variedades
son variedades  tales que
tales que  es isomorfa
es isomorfa  a
a  y
y 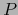 es isomorfa
es isomorfa  a
a  , la variedad
, la variedad 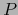 es isomorfa
es isomorfa  a
a  .
.





Siguiente: Producto de variedades
Arriba: Mapas y atlas admisibles.
Anterior: Estructura inducida por un
Guillermo M. Luna
2009-06-14
![]() sobre
sobre ![]() ,
,
![]() es un
atlas admisible de
es un
atlas admisible de ![]() . (En tal caso, lo mismo ocurre para cualquier atlas admisible
. (En tal caso, lo mismo ocurre para cualquier atlas admisible
![]() sobre
sobre ![]() .)
.)
![]() ''.
''.
![]() , se tiene
, se tiene
![]() y
y