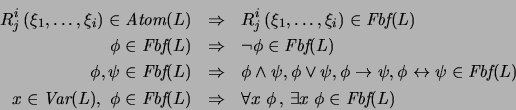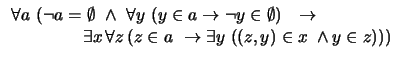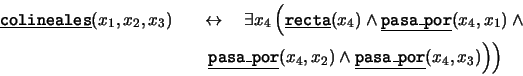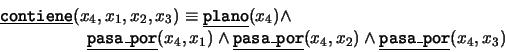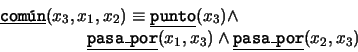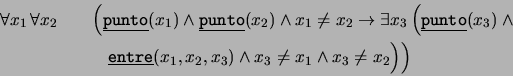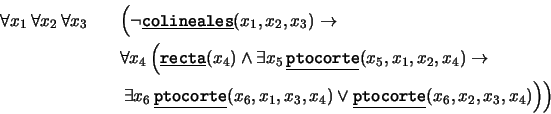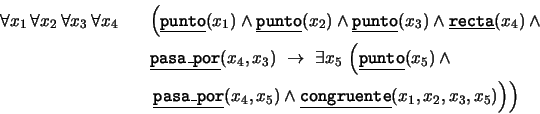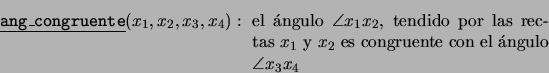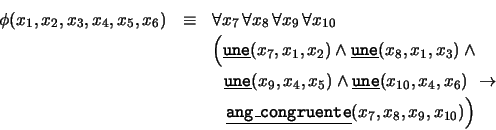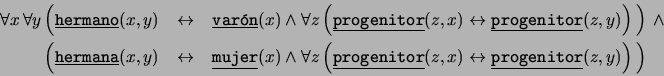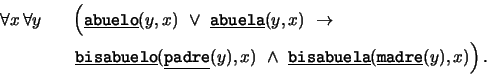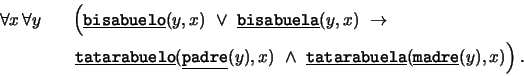Posterior: Semántica
básica del cálculo Arriba: Cálculo de predicados
Anterior: Cálculo de
predicados
El CÁLCULO DE PREDICADOS
difiere del cálculo proposicional en que en él se habla de objetos
o elementos en un dominio. Para predicar
sobre elementos se introducirá variables. En otras
palabras, aquí las fórmulas atómicas no son tan
solo variables proposicionales, como lo eran en el cálculo de
proposiciones, sino que ahora han de ser relaciones en un dominio fijo.
Entremos en detalles técnicos un poco más adelante.
Definición 1.1 Un
ALFABETO 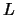 propio
propio para una
TEOR´i
A
DE PRIMER ORDEN es la unión de los
siguientes conjutnos de símbolos:
- Símbolos especiales
-
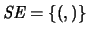
- Conectivos lógicos
-
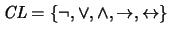
- Cuantificadores
-
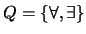 . El símbolo
. El símbolo 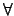 se lee ``para todo'' y se dice ser el CUANTIFICADOR UNIVERSAL y el símbolo
se lee ``para todo'' y se dice ser el CUANTIFICADOR UNIVERSAL y el símbolo  se lee
``existe'' y se dice ser el CUANTIFICADOR EXISTENCIAL.
se lee
``existe'' y se dice ser el CUANTIFICADOR EXISTENCIAL.
- Variables
-
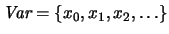
- Símbolos constantes
-
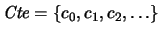
- Símbolos de relaciones
-
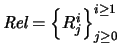 .
.
- Símbolos de funciones
-
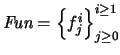 .
.
Los conjuntos de constantes, de relaciones y de funciones han de ser
finitos. La unión de ellos
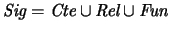
se dice ser la
SIGNATURA de la
teoría. Los superíndices
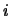
en los
símbolos de relación o de función denotan a su
respectiva
ARIDAD, es decir, al
número de
ARGUMENTOS o de
PLAZAS que involucran.
Así, se tiene que todo alfabeto para una teoría de primer
orden queda prácticamente determinado por su signatura. De
hecho la unión de los otros conjuntos de símbolos, 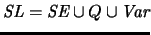 es
común a todos los alfabetos de teorías de primer orden.
El alfabeto con signatura vacía,
es
común a todos los alfabetos de teorías de primer orden.
El alfabeto con signatura vacía, 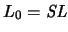 se dice ser el ALFABETO DEL
CÁLCULO DE PREDICADOS PURO. Veamos
algunos ejemplos de alfabetos. En cada caso, describiremos a la
signatura y mencionaremos la connotación que se le dará a
cada símbolo.
se dice ser el ALFABETO DEL
CÁLCULO DE PREDICADOS PURO. Veamos
algunos ejemplos de alfabetos. En cada caso, describiremos a la
signatura y mencionaremos la connotación que se le dará a
cada símbolo.
Ejemplo 1.5 (Parentesco)
Sea
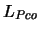
el alfabeto cuya signatura
consta de los símbolos de relación y de función
siguientes:
-
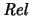 :
:
- Hay símbolos unarios y binarios, cada uno con una
connotación obvia:
- Unarios:
 ,
, 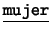 ,
, 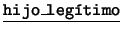 ,
, 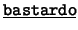 . Cada uno de éstos
es de la forma
. Cada uno de éstos
es de la forma 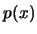 : ``
: `` es
es 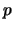 ''.
''.
- Binarios: Cada uno de los siguientes es de la forma
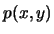
![[*]](footnote.png) : ``
: `` es
es 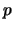 de
de 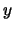 ''. Estos son:
''. Estos son: 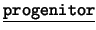 ,
, 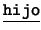 ,
, 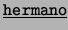 ,
, 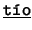 ,
,  ,
, 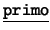 ,
, 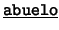 ,
, 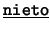 ,
, 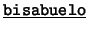 ,
,  ,
,  ,
, 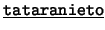 ,
,  ,
, 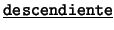 ,
, 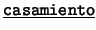 ,
, 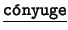 ,
, 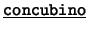 ,
, 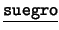 ,
, 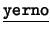 ,
, 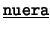 ,
, 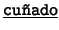 ,
, 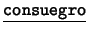 ,
, 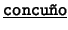 ,
, 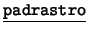 ,
, 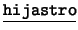 .
.
-
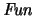 :
:
- Igualmente, hay símbolos unarios y binarios, cada uno con
una connotación obvia:
- Unarios:
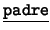 ,
, 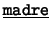 ,
, 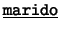 ,
,  ,
, 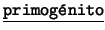 ,
, 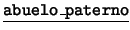 ,
, 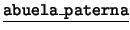 ,
, 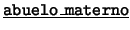 ,
, 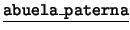 . Cada uno de
éstos es de la forma
. Cada uno de
éstos es de la forma 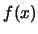 : ``el (la)
: ``el (la) 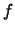 de
de  ''.
''.
- Binarios: Cada uno de los siguientes es de la forma
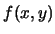 : ``el (la)
: ``el (la) 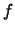 de
de  y de
y de 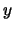 ''. Estos son:
''. Estos son: 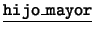 ,
, 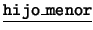 .
.
Ejemplo 1.6 (Geografía política) Sea
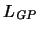
el alfabeto cuya signatura consta
de los símbolos de relación y de función
siguientes:
-
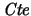 :
:
- Distinguimos dos tipos de constantes. Uno incluye a
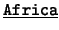 ,
, 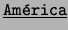 ,
, 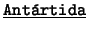 ,
, 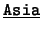 ,
,  ,
, 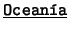 . El otro comprende a la
lista de paises, digamos que inscritos en la FIFA:
. El otro comprende a la
lista de paises, digamos que inscritos en la FIFA: 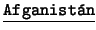 ,
, 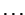 ,
, 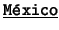 ,
, 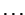 ,
, 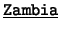 .
.
-
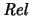 :
:
- Consideramos símbolos unarios y binarios:
- Unarios:
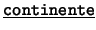 ,
, 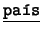 ,
, 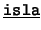 ,
, 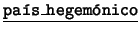 . Cada uno de
éstos es de la forma
. Cada uno de
éstos es de la forma 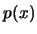 : ``
: `` es
es 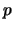 ''.
''.
- Binarios: Cada uno de los siguientes es de la forma
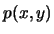 : ``
: ``
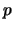
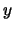 ''.
Estos son:
''.
Estos son: 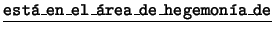 ,
,  ,
,  .
.
-
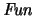 :
:
- Sólo hay símbolos unarios:
- Unarios:
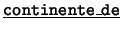 ,
, 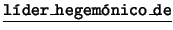 . Cada
uno de éstos es de la forma
. Cada
uno de éstos es de la forma 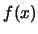 : ``el
: ``el 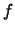
 ''.
''.
La lista de ejemplos podría extenderse arbitrariamente. Como se
desprende de los ejemplos presentados, la parte distintiva de un
alfabeto está constituída, repetimos sólo para
enfatizar, por su signatura. Ahora bien, hemos omitido símbolos
de funciones de aridad 0. Esto es un mero artificio. Si los
introdujéramos, podríamos omitir al conjunto de
constantes pues toda función sin ningunos argumentos puede hacer
las veces de una constante. Esta sutileza es insignificante, y hemos
preferido aquí distinguir propiamente al conjunto de constantes.
Sea pues 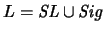 un alfabeto para una
teoría de primer orden, y sea
un alfabeto para una
teoría de primer orden, y sea 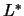 el DICCIONARIO, es decir, el conjunto de palabras de longitud
finita, con símbolos en
el DICCIONARIO, es decir, el conjunto de palabras de longitud
finita, con símbolos en 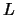 . En
. En 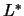 distinguiremos a los conjuntos de términos
y de fórmulas bien formadas.
distinguiremos a los conjuntos de términos
y de fórmulas bien formadas.
Definición 1.2 El conjunto de
TÉRMINOS,
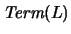
se construye recursivamente como sigue:
- Las variables y las constantes son términos.
- Las funciones aplicadas sobre términos producen nuevos
términos.
Puesto en símbolos:
Por ejemplo, considerando el alfabeto 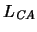 de campos algebraicos,
presentamos algunos términos en la tabla 3.1:
en la primera columna aparecen términos formales y en la segunda
columna la forma en la que los escribimos cotidianamente.
de campos algebraicos,
presentamos algunos términos en la tabla 3.1:
en la primera columna aparecen términos formales y en la segunda
columna la forma en la que los escribimos cotidianamente.
Table: Ejemplos de términos en  .
.
|
|
En el alfabeto de parentesco 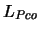 , el término
, el término 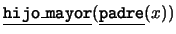 se refiere al ``hermano mayor'' de
se refiere al ``hermano mayor'' de  , el
término
, el
término 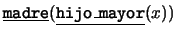 acaso a la ``primera mujer'' de
acaso a la ``primera mujer'' de  , e
, e  al tío mayor de
al tío mayor de  .
.
Definición 1.3 Las
FÓRMULAS
ATÓMICAS, o ´
ATOMOS simplemente, se obtienen de evaluar símbolos de
relación sobre términos:
Por ejemplo, en el alfabeto 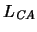 de campos algebraicos, el
átomo
de campos algebraicos, el
átomo
representa la ecuación de segundo grado:
En el lenguaje de parentesco, todo árbol genealógico
representa un conjunto de átomos. En la figura ![[*]](crossref.png) presentamos una célebre
genealogía debida a Gabriel García Márquez,
aquella de sus Cien Años de Soledad. Los átomos
son evidentes. Presentamos únicamente la línea de
descendencia de los Buendía. En caso necesario, presentamos a
los cónyuges.
presentamos una célebre
genealogía debida a Gabriel García Márquez,
aquella de sus Cien Años de Soledad. Los átomos
son evidentes. Presentamos únicamente la línea de
descendencia de los Buendía. En caso necesario, presentamos a
los cónyuges.
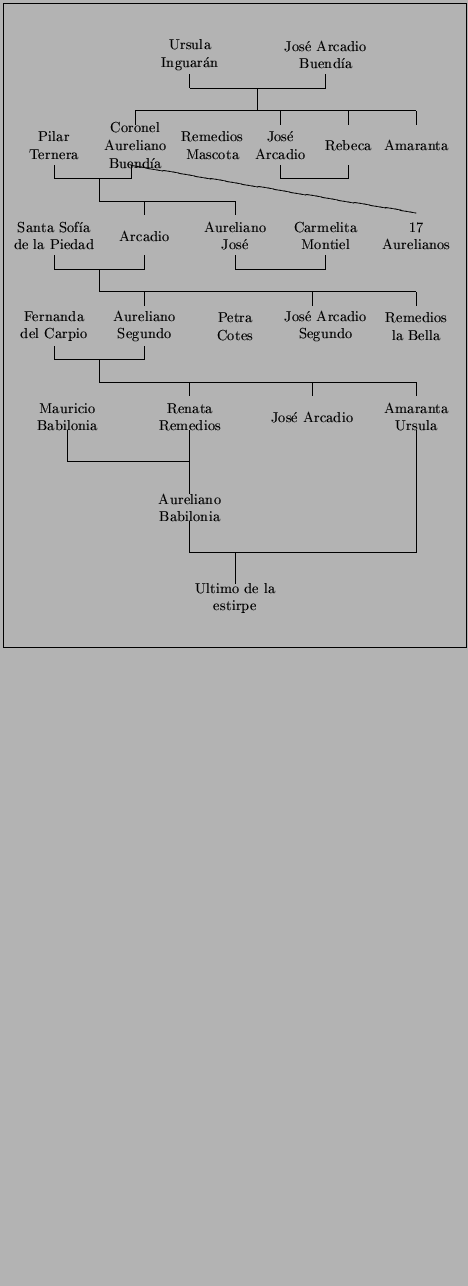
Una estirpe condenada a cien años de soledad.
Definición 1.4 El conjunto de
FÓRMULAS
BIEN FORMADAS,
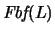
se obtiene partiendo de los átomos,
componiéndolos con los conectivos lógicos y cuantificando
adecuadamente sobre variables: Puesto en símbolos:
La frase adverbial ``de primer orden'' que hasta aquí hemos
aplicado en varias ocasiones a las teorías, se debe a que los
cuantificadores se aplican sólo en un primer orden, es decir,
sólo a las variables. Si introdujéramos variables para
denotar símbolos de relaciones o de funciones, o bien
términos o fórmulas, entonces ``aumentaríamos el
orden de las teorías'' y nos referiríamos a ellas como
teorías de alto orden. En este texto nos restringiremos al
primer orden de cuantificación. Por razones de
precisión en la sintaxis definiremos explícitamente la
aparición, ya sea libre o ligada de una
variable en una fórmula bien formada. Comenzamos definiendo
qué significa que una variable aparezca en un
término.
Pasemos ahora a considerar fórmulas bien formadas.
Así como hay un proceso de deducción natural en el
cálculo proposicional, existe uno en el cálculo de
predicados. Veremos a continuación la noción de demostrabilidad
sintáctica. En ella se tiene una colección de reglas de
inferencia aplicadas, a partir de axiomas, a fórmulas
previamente deducidas para obtener nuevas fórmulas deducidas,
llamadas teoremas. Los axiomas son fórmulas bien
formadas distinguidas, de hecho son enunciados.
Definición 1.7 (Axiomas)
Sea
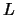
un alfabeto para una teoría de primer
orden. Los
AXIOMAS en
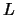
pueden
ser de tres tipos:
AXIOMAS LÓGICOS,
AXIOMAS
DE REESCRITURA y
AXIOMAS
EXTRALÓGICOS. El conjunto de
axiomas
lógicos es
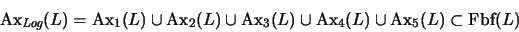 |
(1) |
donde
El conjunto de
axiomas de reescritura es
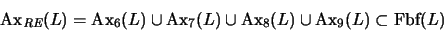 |
(7) |
donde
Los
axiomas extralógicos son propios de una
teoría.
Ejemplifiquemos, para algunos de los alfabetos ya presentados, sistemas
de axiomas extralógicos.
Ejemplo 1.7 (Campos algebraicos) Recordamos que un
CAMPO es una estructura algebraica
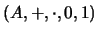
tal que la estructura aditiva
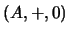
forma un grupo abeliano, el producto
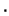
se
distribuye, por ambos lados, respecto a la adición, y la
estructura multiplicativa de elementos no-nulos
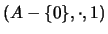
forma un grupo. La noción de campo es
formalizable en una teoría de primer orden.
Explicación. En efecto, a continuación
presentaremos los axiomas de campo. En cada uno, presentamos una
paráfrasis en lenguaje natural, una formulación en
notación de enfijo convencional y el axioma propiamente dicho,
en notación de prefijo formal.
- La adición es asociativa. En notación de
enfijo:
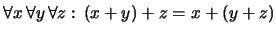 En
notación de prefijo:
En
notación de prefijo: 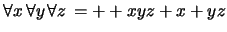
- La adición es conmutativa. En notación de
enfijo:
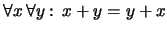 En notación de prefijo:
En notación de prefijo: 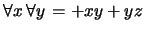
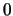 es la unidad aditiva. En notación
de enfijo:
es la unidad aditiva. En notación
de enfijo: 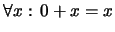 En notación de prefijo:
En notación de prefijo: 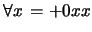
- Cada elemento posee un inverso aditivo. En
notación de enfijo:
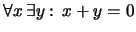 En notación de prefijo:
En notación de prefijo: 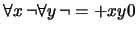
- La multiplicación es asociativa. En
notación de enfijo:
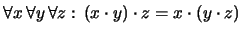 En notación de prefijo:
En notación de prefijo: 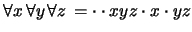
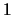 es la unidad multiplicativa. En
notación de enfijo:
es la unidad multiplicativa. En
notación de enfijo: 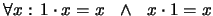 En
notación de prefijo:
En
notación de prefijo: 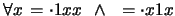
- Cada elemento no-nulo posee un inverso multiplicativo. En
notación de enfijo:
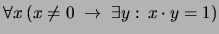 En
notación de prefijo:
En
notación de prefijo: 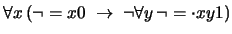
- La multiplicación se distribuye por la izquierda
respecto a la adición. En notación de enfijo:
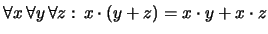 En notación de prefijo:
En notación de prefijo: 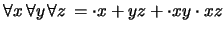
- La multiplicación se distribuye por la derecha
respecto a la adición. En notación de enfijo:
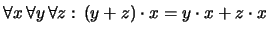 En notación de prefijo:
En notación de prefijo: 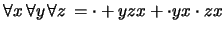
Observamos que en las fórmulas anteriores, cuando aparecen
conectivos lógicos en las formulaciones de prefijos, a
éstos los hemos escrito como operadores de enfijo, con lo cual
nos hemos visto obligados a introducir paréntesis. De hecho esto
se puede evitar escribiendo a los conectivos lógicos en prefijo.
Además como el conjunto de conectivos 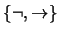 es completo, se podría utilizar
sólo a esos dos conectivos. El cálculo formal de
predicados asume estas convenciones: utiliza sólo a los
conectivos
es completo, se podría utilizar
sólo a esos dos conectivos. El cálculo formal de
predicados asume estas convenciones: utiliza sólo a los
conectivos 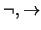 y los escribe en notación de prefijo.
Sin embargo, en Matemáticas se ha tomado el acuerdo
implícito de formularlas en un ``alto nivel'', omitiendo las
anteriores convenciones sintácticas. De acuerdo con esto,
presentaremos los siguientes ejemplos en ese alto nivel, mas el lector
ha de tener en cuenta que éste es traducible, incluso
mecánicamente, a un cálculo de predicados de primer
orden, estrictamente formal.
y los escribe en notación de prefijo.
Sin embargo, en Matemáticas se ha tomado el acuerdo
implícito de formularlas en un ``alto nivel'', omitiendo las
anteriores convenciones sintácticas. De acuerdo con esto,
presentaremos los siguientes ejemplos en ese alto nivel, mas el lector
ha de tener en cuenta que éste es traducible, incluso
mecánicamente, a un cálculo de predicados de primer
orden, estrictamente formal.
Ejemplo 1.8 (Teoría de conjuntos de
Zermelo-Fraenkel) Esta es una teoría que se formula en
el alfabeto
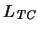
y es formalizable como una
teoría de primer orden.
Explicación. En efecto, de acuerdo con lo planteado
anteriormente, describiremos a sus axiomas extralógicos en un
alto nivel.
Toda la teoría de conjuntos se desprende de estos axiomas.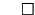
Ejemplo 1.9 (Geometría de Hilbert) En su
libro clásico Fundamentos de Geometría, David
Hilbert plantea una axiomatización de la geometría del
espacio euclidiano de tres dimensiones. Sus axiomas se dividen en tres
grupos: de incidencia, de orden y de congruencia.
Veamos que éstos son formalizables en un primer orden.
Explicación. Planteemos los axiomas divididos por sus
tipos: Axiomas de incidencia.
- ``Para cualesquiera dos puntos dados, existe una única
recta que pasa por ellos'':
- ``Cada recta posee al menos dos puntos'':
- ``Existen tres puntos que no son colineales'': Inicialmente
introduzcamos a una definición como un axioma:
entonces el axioma enunciado es el siguiente:
- ``Por tres puntos que no son colineales pasa un único
plano'': Introduzcamos un predicado:
entonces el axioma queda
- ``Ningún plano es vacío'':
- ``Una recta yace en un plano si al menos dos puntos de la recta
están en el plano'':
- ``Si dos planos se cortan, hay al menos dos puntos comunes a los
planos'': Introduzcamos el predicado:
entonces el axioma queda
- ``Existen cuatro puntos que no son coplanares'': Inicialmente
introduzcamos a una definición como un axioma:
entonces el axioma enunciado es el siguiente:
Axiomas de orden
- ``Si un punto está entre otros dos, entonces los tres son
colineales'':
Aquí se puede introducir también la siguiente
noción de ``simetría'' de la relación ``entre'':
- ``Siempre hay un punto entre otros dos distintos'':
- ``De entre tres puntos colineales distintos hay uno único
que está entre los otros dos'': Introduzcamos un predicado:
entonces el axioma queda
- ``Si una recta corta a un lado de un triángulo, entonces
ha de cortar a un segundo lado de ese triángulo'': Introduzcamos
un predicado que indique que un punto
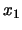 es el de corte
de un segmento
es el de corte
de un segmento 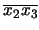 con una recta
con una recta 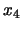 :
:
entonces el axioma queda
Axiomas de congruencia. Congruencia de segmentos:
- ``Para dos puntos en una recta y un tercero en otra,
existirá un cuarto punto en la segunda recta de manera que los
segmentos delimitados por los cuatros puntos dados son congruentes'':
- ``La congruencia de segmentos es transitiva'':
- ``La congruencia de segmentos es aditiva'':
Congruencia de ángulos: Consideraremos aquí una
relación cuaternaria entre rectas:
Los axiomas de congruencia de ángulos son los siguientes:
- ``Dado un ángulo en un plano, una recta en otro plano y un
punto en esta última recta, entonces existen dos rectas en este
segundo plano, que cortan a la recta en el punto dado, cuyos
ángulos con la recta dada son congruentes con el ángulo
dado'':
- ``Si en dos triángulos hay sendos vértices tales
que los lados que se cortan en ellos son correspondientemente
congruentes y los ángulos cuyos vértices son esos puntos
son también congruentes, entonces los ángulos en los
otros vértices son correspondientemente congruentes'': Para
especificar este axioma, introduzcamos primero el predicado ``la recta
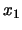 une a los puntos
une a los puntos 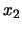 y
y 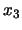 '':
'':
y luego el predicado ``en los triángulos 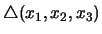 y
y 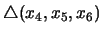 , los ángulos con
vértices
, los ángulos con
vértices 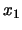 y
y 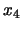 son
congruentes'':
son
congruentes'':
El axioma queda entonces:
Una consecuencia inmediata de este axioma es, por ejemplo, el
célebre
Teorema 1.1 (Pons asnorum (El puente de los asnos))
En todo triángulo isósceles, los ángulos en la
base son congruentes entre sí.
Muchos teoremas clásicos de la llamada geometría
euclidiana resultan de esta axiomatización, por ejemplo, la
existencia de ángulos rectos, el que la suma de los
ángulos internos de un triángulo equivale a dos rectos,
o, inclusive más complejos como el teorema de Papo (Pappus) o el
teorema de Desargues, fundamentales estos últimos en la
geometría proyectiva. 
Ejemplo 1.10 (Relaciones de parentesco) En el
lenguaje
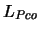
, veremos que las relaciones
comunes de parentesco son formalizables en un primer orden.
Explicación. Éste es efectivamente un ejemplo
más bien frívolo, pero nuestra intención
secundaria para introducirlo aquí es el uso de símbolos
de funciones en los axiomas. El lenguaje 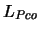 se presentó en el
ejemplo 3.1.5. Parentesco
consanguíneo:
se presentó en el
ejemplo 3.1.5. Parentesco
consanguíneo:
- Comencemos con lo más obvio: ``Todo padre es un
varón y toda madre es una mujer''
- ``Un progenitor de alguien es su padre o su madre.''
- ``Un hijo, resp. hija, de alguien es aquel varón, resp.
mujer, que tiene a ese alguien como progenitor.''
- ``Un hermano, resp. hermana, de alguien es aquel varón,
resp. mujer, que tiene a los mismos progenitores que ese alguien.''
Observe en este caso que los ``medios hermanos'' no son hermanos en el
sentido aquí definido.
- ``Un abuelo, resp. abuela, de alguien es aquel varón,
resp. mujer, que es el padre, resp. madre, de un progenitor de ese
alguien.''
- ``Un bisabuelo, resp. bisabuela, de alguien es el padre, resp.
madre, de un abuelo o de una abuela de ese alguien.''
- ``Un tatarabuelo, resp. tatarabuela, de alguien es el padre,
resp. madre, de un bisabuelo o de una bisabuela de ese alguien.''
- En general, ``un ancestro de alguien es bien uno de sus
progenitores o un ancestro de alguno de sus progenitores.''
- Una definición muy generalizada de parentesco
consanguíneo es la siguiente: ``Dos personas son parientes si
poseen un ancestro común.''
- ``Un tío, resp. tía, es un hermano, resp. hermana,
de uno de sus progenitores.''
- ``Un sobrino, resp. sobrina, de alguien es aquel varón,
resp. mujer, que tiene a ese alguien como tío o tía.''
- ``Un primo, resp. prima, de alguien es un sobrino, resp. sobrina,
de algún progenitor de ese alguien.''
Parentesco político: Otro tipo de parentesco es el que
se establece por el sacrosanto vínculo del matrimonio. Algunas
de estas relaciones son las siguientes:
- ``Toda persona está casada (digamos) con su
cónyuge.''
- ``Si una persona está casada con otra, esta otra
está casada con aquella.''
- ``El cónyuge de una mujer es un varón y la
cónyuge de un varón es una mujer.''
- ``Un concubino es alguien que ha procreado con una sin estar
casado con una.
![[*]](footnote.png) ''
''
- ``Un hijo legítimo es alguien procreado en un
matrimonio.''
- ``Un hijo bastardo es alguien procreado fuera de un matrimonio.''
- ``El suegro, resp. la suegra, es el padre, resp. la madre, del
cónyuge.''
- ``Un cuñado, resp. cuñada, es un hermano, resp.
hermana, del cónyuge, o bien el cónyuge de un hermano o
hermana.''
- ``Un yerno, resp. nuera, es el cónyuge de una hija, resp.
de un hijo.''
- ``Un consuegro, resp. consuegra, es el padre, resp. la madre, de
un yerno o una nuera.''
- ``Concuños son los cónyuges de parejas de
hermanos.''
Aunque se tiene la relación de concuño, es curioso ver
que en castellano no se tiene una relación entre hermanos de
cónyuges.
- ``Un padrastro, resp. madrastra, de alguien es el cónyuge
de la madre, resp. padre, de ese alguien que no es progenitor suyo.''
- ``Un hijastro, resp. hijastra, de alguien es un varón,
resp. mujer, de quien se es padrastro o madrastra.''
Bien que en este ejemplo hemos tratado de presentar exhaustivamente las
nociones de parentesco, seguramente el lector podrá localizar
algunas convencionales que aquí no se presentan, podrá
discrepar con las definiciones aquí presentadas e, incluso,
podrá figurarse algunas presentaciones alternativas como
fórmulas de primer orden. Nos permitimoa aleccionar aquí
al lector a experimentar con diferentes formalizaciones. 



Posterior: Semántica
básica del cálculo Arriba: Cálculo de predicados
Anterior: Cálculo de
predicados
Guillermo
Morales-Luna
2004-07-27
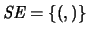
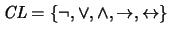
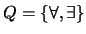 . El símbolo
. El símbolo 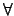 se lee ``para todo'' y se dice ser el CUANTIFICADOR UNIVERSAL y el símbolo
se lee ``para todo'' y se dice ser el CUANTIFICADOR UNIVERSAL y el símbolo  se lee
``existe'' y se dice ser el CUANTIFICADOR EXISTENCIAL.
se lee
``existe'' y se dice ser el CUANTIFICADOR EXISTENCIAL. 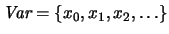
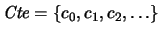
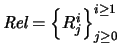 .
. 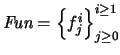 .
. ![[*]](footnote.png)
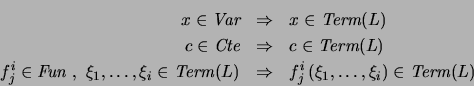
![[*]](crossref.png) presentamos una célebre
genealogía debida a Gabriel García Márquez,
aquella de sus Cien Años de Soledad. Los átomos
son evidentes. Presentamos únicamente la línea de
descendencia de los Buendía. En caso necesario, presentamos a
los cónyuges.
presentamos una célebre
genealogía debida a Gabriel García Márquez,
aquella de sus Cien Años de Soledad. Los átomos
son evidentes. Presentamos únicamente la línea de
descendencia de los Buendía. En caso necesario, presentamos a
los cónyuges.