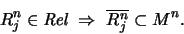Definición 2.1
Sea
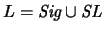
un alfabeto para una teoría
de primer orden, con signatura
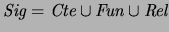
. Una
INTERPRETACIÓN para
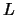
, o una -ESTRUCTURA
, es un conjunto
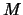
junto con una correspondencia
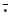
definida en

tal que
- Toda constante corresponde a un elemento en
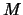 :
:
- Todo símbolo de función de aridad
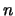 corresponde a una función
corresponde a una función 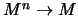 :
:
- Todo símbolo de relación de aridad
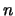 corresponde a una relación de aridad
corresponde a una relación de aridad 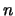 , es decir a un subconjunto en
, es decir a un subconjunto en 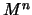 :
:
Diremos que la pareja
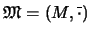
es la interpretación o la
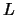
-estructura.
Definición 2.2
Sea
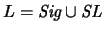
un alfabeto para una teoría
de primer orden, y sea
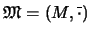
una interpretación. La
INTERPRETACIÓN DE UN TÉRMINO será bien un elemento de
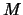
o una función definida en alguna potencia cartesiana de
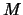
, según el término sea o no cerrado. Explícitamente, para cada término
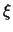
en
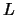
, definimos su interpretación
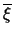
de manera recursiva:
- Si
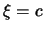 es una constante, entonces
es una constante, entonces
 :
:
- Si
 es una variable, entonces
es una variable, entonces
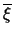 es la función identidad en
es la función identidad en 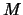 :
:
- Si
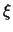 es un término compuesto, entonces
es un término compuesto, entonces
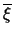 es la composición de las interpretaciones de sus componentes:
es la composición de las interpretaciones de sus componentes:
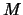 :
:
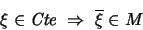
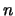 corresponde a una función
corresponde a una función 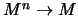 :
:
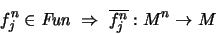
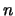 corresponde a una relación de aridad
corresponde a una relación de aridad 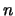 , es decir a un subconjunto en
, es decir a un subconjunto en 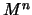 :
: