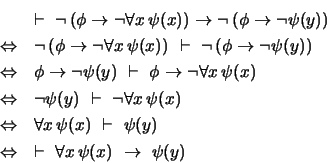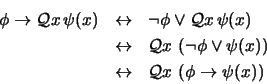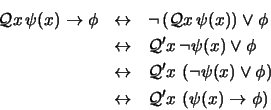

Posterior: Coherencia y completitud
Arriba: Deducción natural en el
Anterior: Camenes
En esta sección presentaremos una forma canónica equivalente de cada fórmula bien formada en el cálculo de predicados. Dada una fórmula, contaremos con un algoritmo que nos permita llevar los cuantificadores que aparezcan en la fórmula al mismo inicio de esa fórmula, de manera que al proceder así con todos los cuantificadores quede un bloque de cuantificadores actuando sobre una fórmula sin cuantificador alguno. Al escribir esta última fórmula en una forma conjuntiva equivalente (que por lo general podemos presuponer que será precisamente la forma normal conjuntiva) obtendremos la forma clausular de la fórmula dada.
Las formas clausulares son de suma importancia porque además de proporcionar un medio canónico de representar a las fórmulas, entrañan también un procedimiento natural para verificar que la fórmula sea válida. Esta última propiedad da orien a su vez a la llamada PROGRAMACIÓN L´OGICA, la cual plantea al cálculo de predicados como un lenguaje de programación.
Inicialmente, probemos la siguiente
Proposición 3.2
Sea
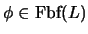
una fórmula donde no aparezca libre la variable
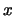
y sea

una segunda fórmula con apariciones libres de
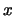
. Entonces en cualquier teoría
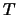
de primer orden:
En esta proposición es importante que 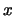 no aparezca libre en
no aparezca libre en  . Por ejemplo, en
. Por ejemplo, en 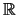 para
para 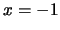 la siguiente fórmula es válida:
la siguiente fórmula es válida:
sin embargo es claramente falsa la fórmula
Demostración
Probemos primeramente la fórmula (7). La fórmula (8) se seguirá entonces por el principio de dualidad. Escribamos las componentes de la equivalencia lógica que aparece en (7) en términos de  y
y  exclusivamente. Obtenemos:
exclusivamente. Obtenemos:
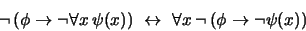 |
(11) |
Pues bien, la implicación 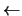 en (11) se reduce a probar que
en (11) se reduce a probar que
lo cual se demuestra como sigue:
- 1.
-
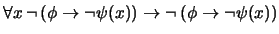 (
(
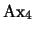 )
)
- 2.
-
 (
(
 )
)
- 3.
-
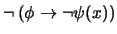 (
(
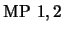 )
)
- 4.
-
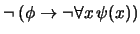 (
(
 )
)
Recíprocamente, para probar la implicación opuesta, procedamos a demostrar:
lo cual puede hacerse como sigue:
- 1.
-
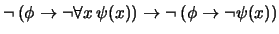 (
(
 )
)
- 2.
-
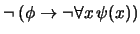 (
(
 )
)
- 3.
-
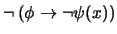 (
(
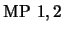 )
)
- 4.
-
 (
(
 )
)
El teorema del que partimos en la prueba anterior, el que aparece en el paso 1. de la prueba, es una consecuencia del Teorema de Deducción. En efecto, se tiene las equivalencias siguientes:
pero esto último se cumple precisamente porque ésta es una instancia del tipo de axiomas
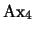 .
.
Probemos ahora la fórmula (9). La fórmula (10) se seguirá entonces por el principio de dualidad. Escribamos las componentes de la equivalencia lógica que aparece en (9) en términos de  y
y  exclusivamente. Obtenemos:
exclusivamente. Obtenemos:
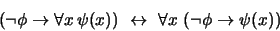 |
(12) |
Pues bien, la implicación 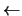 en (12) es una instancia del tipo de axiomas
en (12) es una instancia del tipo de axiomas
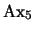 y por tanto es un teorema. La implicación recíproca se obtiene por ``Generalización'' observando que
y por tanto es un teorema. La implicación recíproca se obtiene por ``Generalización'' observando que
como una consecuencia directa de Modus Ponens.
 Si
Si 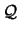 es uno de los cuantificadores
es uno de los cuantificadores 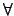 o
o  , sea
, sea 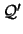 el otro cuantificador, es decir, el cuantificador tal que
el otro cuantificador, es decir, el cuantificador tal que
 .
.
Proposición 3.3
Sea
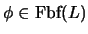
una fórmula donde no aparezca libre la variable
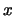
y sea

una segunda fórmula con apariciones libres de
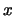
. Entonces en cualquier teoría
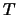
de primer orden:
Demostración
En efecto, teniendo en cuenta las equivalencias lógicas enunciadas en la proposición 3.3.2, para (13), se tiene:
Para (14), se tiene:

Definición 3.5
Sea

una fórmula
libre de cuantificadores (es decir, no contiene cuantificador alguno). Como en el cálculo proposicional, se dice que
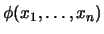
es una
literal si es un átomo o la negación de un átomo. Una conjunción de literales es una
frase y una disyunción de literales es una
cláusula. Una
forma conjuntiva es una conjunción de cláusulas y una
forma disyuntiva es una disyunción de frases.
Proposición 3.4
Si
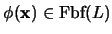
es una fórmula libre de cuantificadores, donde
![$\mbox{\bf x}=[x_1,\ldots,x_n]$](img714.png)
es la lista de sus variables, entonces se puede encontrar algorítmicamente sendas fórmulas
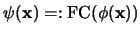
en forma conjuntiva y
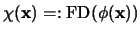
en forma disyuntiva equivalentes ambas a

.
Demostración
En efecto, procedamos por inducción en el número  de conectivos presentes en
de conectivos presentes en
 .
.
Caso base. (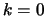 ) Si
) Si
 es un átomo, hacemos
es un átomo, hacemos
Caso inductivo. ( ) Sea
) Sea 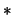 el conectivo principal en
el conectivo principal en
 .
.
Si 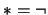 es la negación, entonces
es la negación, entonces
 , y, según las Leyes de De Morgan:
, y, según las Leyes de De Morgan:
-
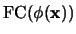 se obtiene de
se obtiene de
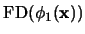 al intercambiar cada conectivo
al intercambiar cada conectivo 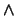 por
por 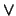 y viceversa, negando cada literal.
y viceversa, negando cada literal.
-
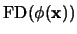 se obtiene de
se obtiene de
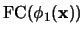 al intercambiar cada conectivo
al intercambiar cada conectivo 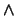 por
por 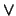 y viceversa, negando cada literal.
y viceversa, negando cada literal.
Si 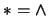 es la conjunción, entonces
es la conjunción, entonces
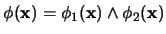 , y:
, y:
-
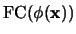 se obtiene al concatenar
se obtiene al concatenar
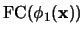 y
y
 , vistos ambos como ``listas'' de cláusulas.
, vistos ambos como ``listas'' de cláusulas.
-
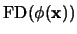 se obtiene como la lista de frases formadas al concatenar cada frase en
se obtiene como la lista de frases formadas al concatenar cada frase en
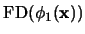 con cada frase en
con cada frase en
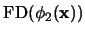 .
.
Si 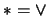 es la disyunción, entonces
es la disyunción, entonces
 , y:
, y:
-
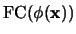 se obtiene como la lista de cláusulas formadas al concatenar cada cláusula en
se obtiene como la lista de cláusulas formadas al concatenar cada cláusula en
 con cada cláusula en
con cada cláusula en
 .
.
-
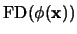 se obtiene al concatenar
se obtiene al concatenar
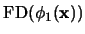 y
y
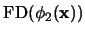 , vistos ambos como ``listas'' de frases.
, vistos ambos como ``listas'' de frases.
en cualquier otro caso, se reescribe 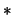 en su forma equivalente en términos de los conectivos booleanos
en su forma equivalente en términos de los conectivos booleanos  ,
, 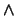 o
o 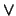 y se calcula las formas conjuntiva y disyuntiva de la fórmula equivalente.
y se calcula las formas conjuntiva y disyuntiva de la fórmula equivalente. 
Definición 3.6
Una fórmula

se dice estar en
FORMA PRENEX si es de la forma
donde cada
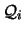
es un cuantificador
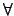
o

, y

es una fórmula libre de cuantificadores. Si además
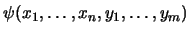
es una forma conjuntiva, entonces se dice que
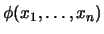
está en
FORMA NORMAL PRENEX.
Así en una forma prenex, los cuantificadores sólo aparecen al inicio de ella.
Proposición 3.5
Para toda fórmula
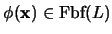
, donde
![$\mbox{\bf x}=[x_1,\ldots,x_n]$](img714.png)
es la lista de sus variables libres, existe una fórmula
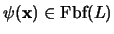
en forma normal prenex equivalente a

. Más aún,

es algorítmicamente constructible a partir de

.
Demostración
Procederemos por inducción en cuanto al número  de cuantificadores que aparezcan en
de cuantificadores que aparezcan en
 .
.
Caso base. (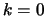 ) Si
) Si
 es una fórmula libre de cuantificadores, calculamos
es una fórmula libre de cuantificadores, calculamos
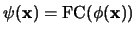 según se vió en la demostración de la proposición 3.3.4.
según se vió en la demostración de la proposición 3.3.4.
Caso inductivo. ( ) Distinguiremos casos diversos atendiendo a la forma de
) Distinguiremos casos diversos atendiendo a la forma de
 .
.
Si
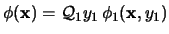 es la cuantificación de una fórmula, entonces se calcula la forma normal prenex
es la cuantificación de una fórmula, entonces se calcula la forma normal prenex
 de
de
 . La forma normal buscada será
. La forma normal buscada será
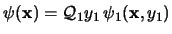 .
.
Si
 es la negación de una fórmula, entonces se hace ``actuar
es la negación de una fórmula, entonces se hace ``actuar  al nivel de átomos''. Es decir, mediante las reglas de transformación:
al nivel de átomos''. Es decir, mediante las reglas de transformación:
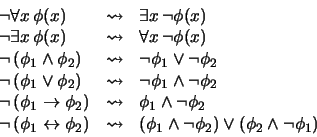 |
(15) |
se transforma
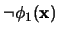 a una fórmula
a una fórmula
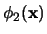 equivalente cuyo conectivo principal ya no es
equivalente cuyo conectivo principal ya no es  . La fórmula
. La fórmula
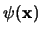 buscada será la forma normal prenex de
buscada será la forma normal prenex de
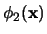 .
.
Si
 es una composición booleana de dos fórmulas, donde
es una composición booleana de dos fórmulas, donde 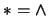 o
o 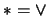 , entonces se puede suponer que
, entonces se puede suponer que
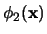 posee un cuantificador (si fuera necesario podría intercambiarse a
posee un cuantificador (si fuera necesario podría intercambiarse a
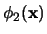 con
con
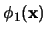 ), digamos
), digamos
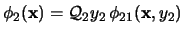 . Ya que
. Ya que  no aparece en la lista de variables libres
no aparece en la lista de variables libres 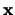 , si acaso
, si acaso  aparece también en
aparece también en
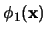 entonces aparecería ahí como una variable ligada. En este caso renombramos a
entonces aparecería ahí como una variable ligada. En este caso renombramos a  , en su alcance en
, en su alcance en
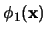 , como una nueva variable
, como una nueva variable 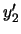 de manera que
de manera que  , en suma, no aparezca más en
, en suma, no aparezca más en
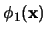 . De acuerdo con la proposición 3.3.2,
. De acuerdo con la proposición 3.3.2,
 es entonces equivalente a
es entonces equivalente a
 y la fórmula
y la fórmula
 posee un cuantificador menos. Sea pues
posee un cuantificador menos. Sea pues
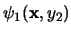 su forma normal prenex. Entonces la forma normal prenex de
su forma normal prenex. Entonces la forma normal prenex de
 será
será
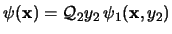 .
.
Si
 es una implicación de dos fórmulas, entonces una de las dos (o incluso ambas)
es una implicación de dos fórmulas, entonces una de las dos (o incluso ambas)
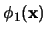 o
o
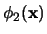 posee un cuantificador.
Si acaso
posee un cuantificador.
Si acaso
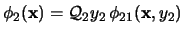 podemos suponer (acaso mediante un renombramiento de variables) que
podemos suponer (acaso mediante un renombramiento de variables) que  no aparece en
no aparece en
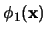 . De acuerdo con la relación (13) en la proposición 3.3.3,
. De acuerdo con la relación (13) en la proposición 3.3.3,
 es entonces equivalente a
es entonces equivalente a
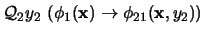 y la fórmula
y la fórmula
 posee un cuanificador menos. Sea pues
posee un cuanificador menos. Sea pues
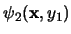 su forma normal prenex. Entonces la forma normal prenex de
su forma normal prenex. Entonces la forma normal prenex de
 será
será
 .
Si acaso
.
Si acaso
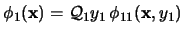 podemos suponer (acaso mediante un renombramiento de variables) que
podemos suponer (acaso mediante un renombramiento de variables) que 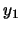 no aparece en
no aparece en
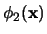 . De acuerdo con la relación (14) en la proposición 3.3.3,
. De acuerdo con la relación (14) en la proposición 3.3.3,
 es entonces equivalente a
es entonces equivalente a
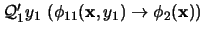 y la fórmula
y la fórmula
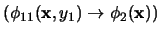 posee un cuanificador menos. Sea pues
posee un cuanificador menos. Sea pues
 su forma normal prenex. Entonces la forma normal prenex de
su forma normal prenex. Entonces la forma normal prenex de
 será
será
 .
. 


Posterior: Coherencia y completitud
Arriba: Deducción natural en el
Anterior: Camenes
Guillermo Morales-Luna
2004-07-27