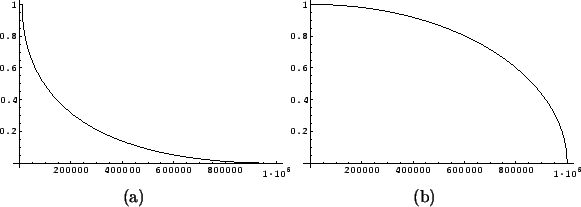
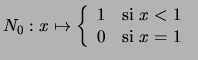 . Su gráfica se ve en la figura 4.9 (a).
. Su gráfica se ve en la figura 4.9 (a).
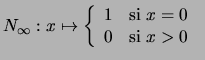 . Su gráfica se ve en la figura 4.9 (b).
. Su gráfica se ve en la figura 4.9 (b).
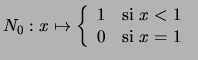 . Su gráfica se ve en la figura 4.9 (a).
. Su gráfica se ve en la figura 4.9 (a).
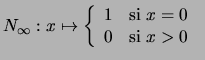 . Su gráfica se ve en la figura 4.9 (b).
. Su gráfica se ve en la figura 4.9 (b).
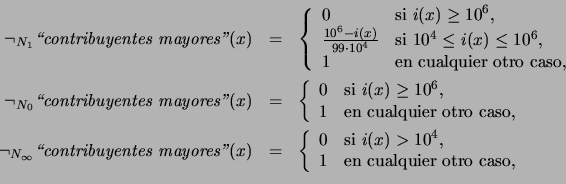
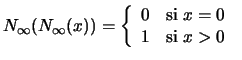 Para todo conjunto difuso
Para todo conjunto difuso 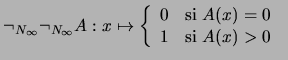
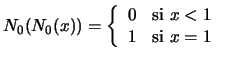 Para todo conjunto difuso
Para todo conjunto difuso 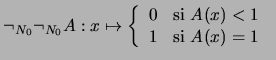
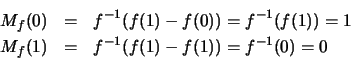
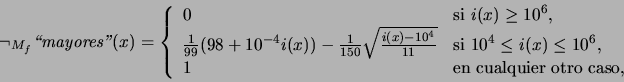
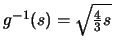 y consecuentemente
y consecuentemente
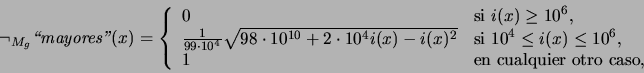
 |