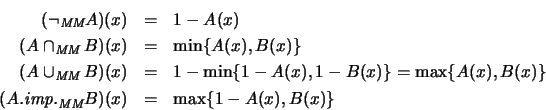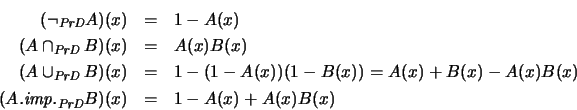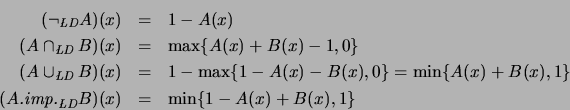

Posterior: Productos cartesianos
Arriba: Operadores composicionales
Anterior: Negaciones
Las operaciones conjuntistas usuales pueden ponerse en función de
algunas otras operaciones distinguidas.
Recordamos que una colección de operadores en conjuntos se dice ser
completa si cualquier otro operador conjuntista se expresa en términos
de los operadores en esa colección.
En efecto, utilizando propiedades de álgebra booleana, de entre ellas a
las leyes de De Morgan de manera principal,
- en términos de
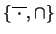 se tiene
se tiene
- en términos de
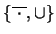 se tiene
se tiene
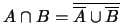 y, por el punto anterior, esto
basta para tener lo aseverado,
y, por el punto anterior, esto
basta para tener lo aseverado,
- en términos de
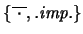 se tiene
se tiene
 y, por el punto anterior, esto basta para tener lo aseverado,
y, por el punto anterior, esto basta para tener lo aseverado,
- en términos de
 se tiene
se tiene
y como
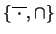 es completo se tiene lo
aseverado,
es completo se tiene lo
aseverado,
- en términos de
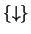 se tiene
se tiene
y como
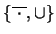 es completo se
tiene lo aseverado.
es completo se
tiene lo aseverado.
Basta pues definir un conjunto completo de operadores para describir luego
a los otros operadores conjuntistas en términos de los ya definidos.
Usaremos esto como estrategia para extender las operaciones conjuntistas a
los conjuntos difusos: extenderemos las operaciones en un conjunto dado
completo de conectivos y luego obtendremos las extensiones de los demás
operadores en función de las extensiones que hagamos de los operadores
que aparezcan en el conjunto completo.
Procederemos ahora a introducir operadores que extiendan a los usuales de
intersección y unión. Observemos que la intersección usual es
asociativa, conmutativa, monótona en cada uno de sus factores, es decir,
y además el universo 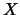 es una unidad, en
tanto que su complemento
es una unidad, en
tanto que su complemento 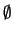 es un anulador, o sea
es un anulador, o sea
Generalicemos estas propiedades.
Un operador
![$\diamond:[0,1]\rightarrow [0,1]$](img257.png) es un
conjuntor
es un
conjuntor![[*]](footnote.png) si se cumplen las propiedades
siguientes:
si se cumplen las propiedades
siguientes:
Un
operador conjuntor determina un operador de intersección de
conjuntos difusos. Si, por otro lado,
![$N:[0,1]\rightarrow[0,1]$](img259.png) es una
negación entonces, de acuerdo con el lema (4.2.3), ya que la
intersección junto con el complemento forman un conjunto completo de
conectivos, se puede definir a los demás en términos de ellos.
Veamos algunos ejemplos.
es una
negación entonces, de acuerdo con el lema (4.2.3), ya que la
intersección junto con el complemento forman un conjunto completo de
conectivos, se puede definir a los demás en términos de ellos.
Veamos algunos ejemplos.
- Min-Max.
- Sea
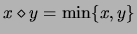 y
y
 . Entonces
. Entonces  es, en efecto, un operador
conjuntor y,
es, en efecto, un operador
conjuntor y,
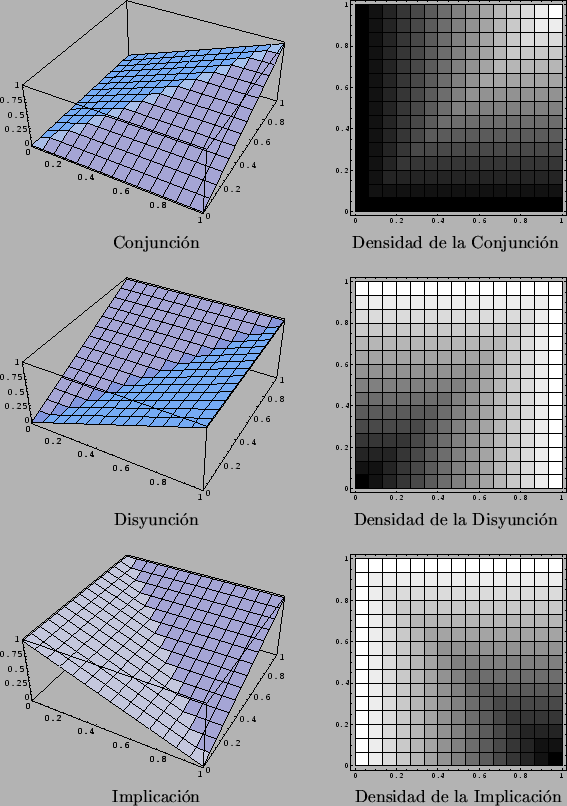
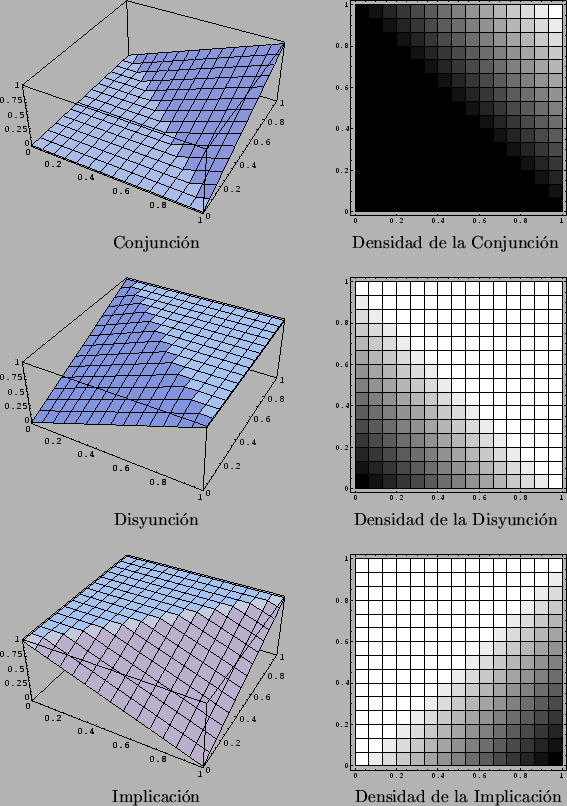
En la figura 4.13 presentamos las gráficas de estas funciones. Las
que aparecen en el lado derecho, son del tipo llamado ``de densidad'', que son
gráficas a vista de pájaro, donde los menores valores corresponden al color negro.
Figure 4.13:
Operadores composicionales del tipo Max-Min.
 |
- Producto-D.
- Sea
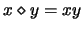 y
y
 . Entonces
. Entonces  es, en efecto, un operador
conjuntor y,
es, en efecto, un operador
conjuntor y,
En la figura 4.14 presentamos las gráficas de estas funciones.
Figure 4.14:
Operadores composicionales del tipo Producto-D.
 |
 ukasiewicz-D.
ukasiewicz-D.- Sea
 y
y
 . Entonces
. Entonces  es, en efecto, un operador
conjuntor y,
es, en efecto, un operador
conjuntor y,
En la figura 4.15 presentamos las gráficas de estas funciones.
Figure:
Operadores composicionales del tipo ukasiewicz-D.
 |
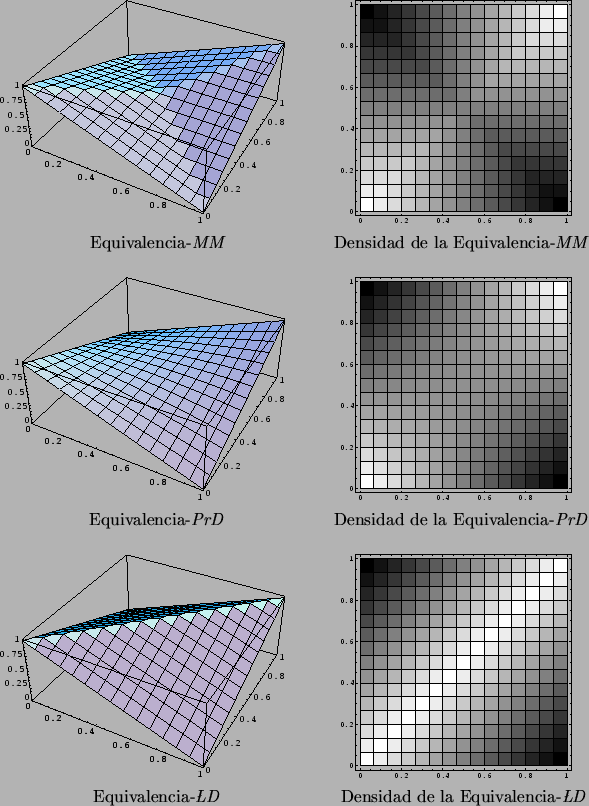
En cada uno de los tres conjuntos de conectivos anteriores se define también uno
de ``equivalencia lógica'':
Las gráficas de las funciones resultantes se muestran en la figura 4.16.
Figure 4.16:
Operadores de equivalencia lógica.
 |
Con cada clase de conectivos, los conjuntos difusos forman una estructura
algebraica que, sin ser un álgebra booleana, posee varias de las
propiedades características de estas últimas. Veremos más adelante que una
estructura algebraica típica conformada por los conjuntos difusos es la de un
``retículo residual''.


Posterior: Productos cartesianos
Arriba: Operadores composicionales
Anterior: Negaciones
Guillermo Morales-Luna
2004-07-28
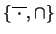 es completo, donde
es completo, donde
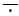 denota a la operación complemento.
denota a la operación complemento.
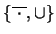 es completo.
es completo.
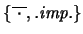 es completo,
donde
es completo,
donde
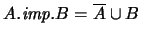 .
.
 es completo, donde
es completo, donde
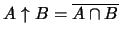 es el
complemento de la intersección.
es el
complemento de la intersección.
 es completo, donde
es completo, donde
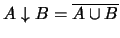 es el complemento de la unión.
es el complemento de la unión.
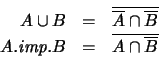
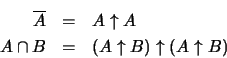

![[*]](footnote.png) si se cumplen las propiedades
siguientes:
si se cumplen las propiedades
siguientes: ![\begin{displaymath}\begin{array}{lccc} \forall x,y\in[0,1]: &\ &\ & x\diamond
y...
...\forall x\in[0,1]: &1\diamond x=x &,& 0\diamond x=0 \end{array}\end{displaymath}](img258.png)