

Posterior: Etiquetas lingüísticas
Arriba: Operadores composicionales
Anterior: Operadores binarios
Recordamos que para dos conjuntos usuales 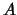 ,
, 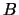 su producto
cartesiano consta de todas las parejas ordenadas de la forma
su producto
cartesiano consta de todas las parejas ordenadas de la forma 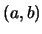 donde
donde 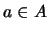 y
y 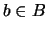 . Así pues, si
. Así pues, si 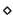 es un
operador conjuntor y
es un
operador conjuntor y 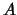 y
y 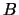 son conjuntos difusos en sendos universos
son conjuntos difusos en sendos universos
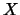 e
e 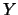 , su producto cartesiano es el conjunto difuso
, su producto cartesiano es el conjunto difuso
Una relación, en el sentido usual, entre dos conjuntos es un
subconjunto de su producto cartesiano. Por tanto, se puede considerar a
una relación difusa entre dos universos como un conjunto difuso en
su producto cartesiano.
Ejemplo: Para ![$X=[0,1]$](img172.png) , el conjunto difuso en
, el conjunto difuso en 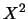 ,
,
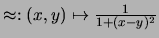 puede ser visto como la
relación difusa ``aproximadamente igual''. Mostramos su gráfica en la
figura 4.17.
puede ser visto como la
relación difusa ``aproximadamente igual''. Mostramos su gráfica en la
figura 4.17.
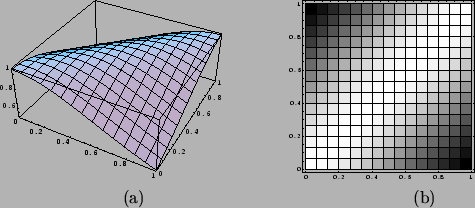
Figure 4.17:
(a) Gráfica de la relación ``aproximadamente
igual''.
(b) Gráfica de densidad de la relación ``aproximadamente
igual''.
 |
Si 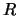 es una relación difusa en
es una relación difusa en 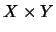 , las respectivas
proyecciones de
, las respectivas
proyecciones de 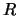 en
en 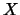 y en
y en 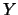 son los conjuntos difusos
son los conjuntos difusos
Si 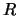 es una relación difusa en
es una relación difusa en 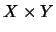 y
y 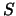 es una relación
difusa en
es una relación
difusa en 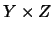 , la composición de
, la composición de 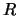 con
con 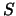 en
en 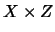 es el conjunto difuso
es el conjunto difuso
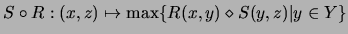 .
.
Ejemplo: Consideremos un conjunto de 10 chicos,
y otro de 10
chicas
Una relación difusa, llamémosla Prefiere_A, del conjunto de
Chicos sobre el conjunto de Chicas se muestra en el
recuadro (4.6).
Table 4.6:
Relación Prefiere_A de
Chicos a Chicas.
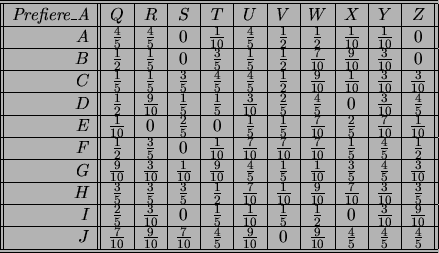 |
En esa
relación, un chico preferirá más a una chica si el correspondiente
valor de esa pareja es más cercano a 1. Si es 0, el chico
definitivamente no prefiere a la chica. Juan, por ejemplo, a ninguna
prefiere más que a Rosa, a Ursula y a Wanda, pero a
ellas tres las prefiere por igual (aunque él de hecho está
manifestando cualquier preferencia con mucho ímpetu). Sofía
es acaso de las menos preferidas, y Abel, Beto, Felipe e
Ignacio para nada la prefieren.
Pero, obviamente, ¡las chicas también tienen sus preferencias!
Consideremos la relación Elige_A de Chicas en Chicos
que se muestra en el recuadro (4.7).
Table 4.7:
Relación Elige_A de Chicas a Chicos.
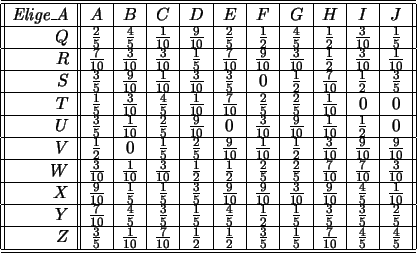 |
En las relaciones definidas, se tiene, por ejemplo, que Beto
prefiere más a Xóchitl pero ella elige más a Abel,
Ernesto, Felipe y Héctor.
La composición
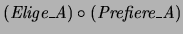 , llamémosla
Siéntese_Rival_De (SRD), es una relación de Chicos en
Chicos: Fulano Siéntese_Rival_De Zutano si la chica que
más prefiere Fulano elige más a Zutano. Utilizando como conjuntor a la
operación
, llamémosla
Siéntese_Rival_De (SRD), es una relación de Chicos en
Chicos: Fulano Siéntese_Rival_De Zutano si la chica que
más prefiere Fulano elige más a Zutano. Utilizando como conjuntor a la
operación 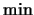 se tiene la relación mostrada en el
recuadro (4.8).
se tiene la relación mostrada en el
recuadro (4.8).
Table:
Relación
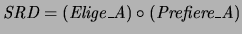 de Chicos a Chicos.
de Chicos a Chicos.
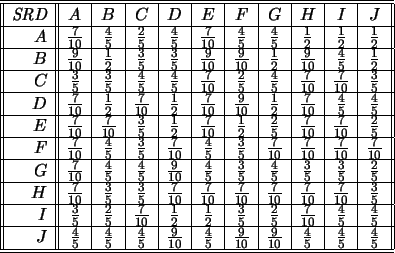 |
La terminología es desafortunada pues, por ejemplo, Chucho SRD
de sí mismo (lo que es muy bueno). El prefiere más que a nadie a
Wanda, pero ella no se muestra muy afecta a los chicos propuestos.
En cambio, Chucho y Teresa se atraen recíprocamente con
0.8. Por otro lado, Juan quiere tanto a todas las chicas, menos a
Virginia, que SRD de cualquier otro chico.
Finalmente, la composición
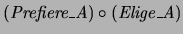 ,
llamémosla Celosa_De (CD), es una relación de Chicas en
Chicas. Se tiene la relación mostrada en el
recuadro (4.9).
,
llamémosla Celosa_De (CD), es una relación de Chicas en
Chicas. Se tiene la relación mostrada en el
recuadro (4.9).
Table:
Relación
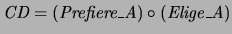 de Chicas a Chicas.
de Chicas a Chicas.
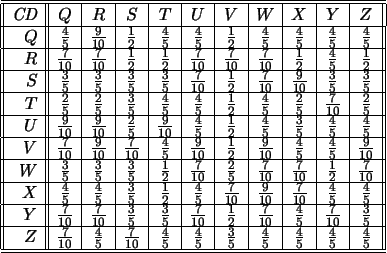 |
Virginia está muy descontenta consigo misma,
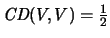 , porque los tres chicos que elegiría más
la prefieren a ella menos que a las demás.
Sírvame como disculpa de la banalidad de este ejemplo, el mencionar
que corresponde a un planteamiento típico de los problemas dichos de
``Matrimonios Estables'' (en inglés ``Stable Marriage Problems''),
los cuales aparecen frecuentemente como problemas de planeación. Si se
piensa que los chicos son ``clientes'' y las chicas
``servidores''
, porque los tres chicos que elegiría más
la prefieren a ella menos que a las demás.
Sírvame como disculpa de la banalidad de este ejemplo, el mencionar
que corresponde a un planteamiento típico de los problemas dichos de
``Matrimonios Estables'' (en inglés ``Stable Marriage Problems''),
los cuales aparecen frecuentemente como problemas de planeación. Si se
piensa que los chicos son ``clientes'' y las chicas
``servidores''![[*]](footnote.png) entonces se ha de buscar una asignación
donde los clientes y los servidores creen entre ellos los mínimos
conflictos posibles, si hubiese que crearlos. En algunas aplicaciones, los
clientes y los servidores son ``clientes de una empresa'' y ``funcionarios
de la empresa'', respectivamente, o bien ``clientes en colas'' y
``despachadores de las colas'', o bien ``tareas'' y ``procesadores'', o
bien ``tesistas'' y ``directores de tesis'', o bien ``cursos'' y
``aulas'', o bien ``aspirantes a ingresar al bachillerato'' y ``escuelas
de bachilleres disponibles'', etc.
entonces se ha de buscar una asignación
donde los clientes y los servidores creen entre ellos los mínimos
conflictos posibles, si hubiese que crearlos. En algunas aplicaciones, los
clientes y los servidores son ``clientes de una empresa'' y ``funcionarios
de la empresa'', respectivamente, o bien ``clientes en colas'' y
``despachadores de las colas'', o bien ``tareas'' y ``procesadores'', o
bien ``tesistas'' y ``directores de tesis'', o bien ``cursos'' y
``aulas'', o bien ``aspirantes a ingresar al bachillerato'' y ``escuelas
de bachilleres disponibles'', etc. 
Si 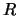 es una relación difusa en
es una relación difusa en 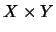 , entonces todo conjunto
difuso
, entonces todo conjunto
difuso 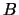 en
en 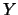 determina un conjunto difuso
determina un conjunto difuso 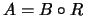 en
en 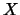 como
como
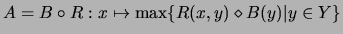 .
. 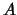 se dice ser
la composición de
se dice ser
la composición de 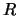 con
con 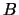 .
.


Posterior: Etiquetas lingüísticas
Arriba: Operadores composicionales
Anterior: Operadores binarios
Guillermo Morales-Luna
2004-07-28

![\begin{eqnarray*}\pi_X[R]:x &\mapsto& \max\{R(x,y)\vert y\in Y\}, \\
\pi_Y[R]:y &\mapsto& \max\{R(x,y)\vert x\in X\}. \end{eqnarray*}](img283.png)
![\begin{displaymath}\mbox{\it Chicos}\ =\
\{\mbox{\rm\begin{minipage}[t]{30em} {...
...
Felipe, Guillermo, H\'ector, Ignacio, Juan } \}\end{minipage}}\end{displaymath}](img288.png)
![\begin{displaymath}\mbox{\it Chicas}\ =\ \{\mbox{\rm\begin{minipage}[t]{30em} {\...
...rginia, Wanda, X\'ochitl, Yolanda, Zenaida }
\}\end{minipage}}\end{displaymath}](img289.png)
![[*]](footnote.png) entonces se ha de buscar una asignación
donde los clientes y los servidores creen entre ellos los mínimos
conflictos posibles, si hubiese que crearlos. En algunas aplicaciones, los
clientes y los servidores son ``clientes de una empresa'' y ``funcionarios
de la empresa'', respectivamente, o bien ``clientes en colas'' y
``despachadores de las colas'', o bien ``tareas'' y ``procesadores'', o
bien ``tesistas'' y ``directores de tesis'', o bien ``cursos'' y
``aulas'', o bien ``aspirantes a ingresar al bachillerato'' y ``escuelas
de bachilleres disponibles'', etc.
entonces se ha de buscar una asignación
donde los clientes y los servidores creen entre ellos los mínimos
conflictos posibles, si hubiese que crearlos. En algunas aplicaciones, los
clientes y los servidores son ``clientes de una empresa'' y ``funcionarios
de la empresa'', respectivamente, o bien ``clientes en colas'' y
``despachadores de las colas'', o bien ``tareas'' y ``procesadores'', o
bien ``tesistas'' y ``directores de tesis'', o bien ``cursos'' y
``aulas'', o bien ``aspirantes a ingresar al bachillerato'' y ``escuelas
de bachilleres disponibles'', etc.