 una función de apareamiento. Definimos inductivamente
una función de apareamiento. Definimos inductivamente
 como sigue
como sigue
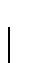 se define de manera que
se define de manera que
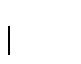 :
:
 como
como
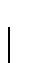 puede escribirse como
puede escribirse como
 ,
donde
,
donde
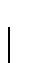 se calcula por un programa-while con a lo sumo p variables.
se calcula por un programa-while con a lo sumo p variables.
 es una ``reiteración'' de a lo sumo n-j+1 proyecciones de a. Supongamos que Q1a y Q2a sean sendos programas-while que calculan a las proyecciones
es una ``reiteración'' de a lo sumo n-j+1 proyecciones de a. Supongamos que Q1a y Q2a sean sendos programas-while que calculan a las proyecciones
|
|
![\fbox{\begin{minipage}[t]{20em}
\begin{tabbing}123\=456\=789\=012\=345\=678\=901...
...e ; \\
(*)\> $Z:=\mbox{\it Aux}1$\space \\
\}
\end{tabbing}
\end{minipage}}](img641.gif) |