 .
.
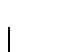 posee una cinta semi-infinita. En su primera parte ha de escribir el código de cualquier máquina M que ha de simular, llamemos a esta parte área de programa. Aparece luego el área de trabajo. Aunque esta porción de la cinta de
posee una cinta semi-infinita. En su primera parte ha de escribir el código de cualquier máquina M que ha de simular, llamemos a esta parte área de programa. Aparece luego el área de trabajo. Aunque esta porción de la cinta de
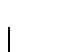 es semi-infinita, se puede suponer que se tiene la cinta infinita a ambos lados módulo la reducción de máquinas de Turing a máquinas con cinta semi-infinita vista en el primer capítulo. Así que cualesquiera movimientos en
es semi-infinita, se puede suponer que se tiene la cinta infinita a ambos lados módulo la reducción de máquinas de Turing a máquinas con cinta semi-infinita vista en el primer capítulo. Así que cualesquiera movimientos en
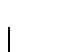 han de interpretarse como movimientos módulo aquella reducción. Incorporemos en
han de interpretarse como movimientos módulo aquella reducción. Incorporemos en
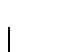 a las quíntuplas necesarias para hacer corrimientos a la derecha y a la izquierda, y para sustituir una cadena por otra. Acaso en este punto será necesario introducir algunos ``apuntadores'' de corrimientos. Además introduciremos símbolos especiales para utilizarlos como delimitador izquierdo del contenido del área de trabajo, delimitador derecho de ese contenido, ``cabeza lectora'' de la máquina M y apuntador a la ``quintupla activa'' en el código de M.
Cuando comienza funcionar
a las quíntuplas necesarias para hacer corrimientos a la derecha y a la izquierda, y para sustituir una cadena por otra. Acaso en este punto será necesario introducir algunos ``apuntadores'' de corrimientos. Además introduciremos símbolos especiales para utilizarlos como delimitador izquierdo del contenido del área de trabajo, delimitador derecho de ese contenido, ``cabeza lectora'' de la máquina M y apuntador a la ``quintupla activa'' en el código de M.
Cuando comienza funcionar
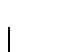 ,
en su área de programa se encuentra el código de una máquina M y en el área de trabajo se encuentra el código de los datos
,
en su área de programa se encuentra el código de una máquina M y en el área de trabajo se encuentra el código de los datos
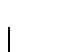 ha de aplicar el efecto de M.
El funcionamiento de
ha de aplicar el efecto de M.
El funcionamiento de
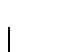 se resume más abajo. Reiteramos aquí que
se resume más abajo. Reiteramos aquí que
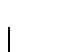 trabaja sobre códigos. Aunque en la presentación nos referiremos a los símbolos originales, el lector ha de tener en cuenta que, en realidad, son los códigos de esos símbolos los objetos de los que se está hablando.
trabaja sobre códigos. Aunque en la presentación nos referiremos a los símbolos originales, el lector ha de tener en cuenta que, en realidad, son los códigos de esos símbolos los objetos de los que se está hablando.
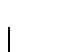 .
Ahora, la simulación anterior, puede realizarse con una máquina de Turing de una sola cinta, según se vió en el primer capítulo. Resulta entonces que se cumplen las siguientes dos proposiciones,
.
Ahora, la simulación anterior, puede realizarse con una máquina de Turing de una sola cinta, según se vió en el primer capítulo. Resulta entonces que se cumplen las siguientes dos proposiciones,