La operación de desdifusificar5, u operación-DF para abreviar, consiste en seleccionar un elemento
representativo de un conjunto difuso. Con esta operación ``se suprime lo
difuso'' porque habiendo estimado propiedades de un conjunto difuso, se
elige a un objeto ``concreto'' que lo representa. Para esto, existen
diversos criterios.
Primer máximo
Tómese como representante de un conjunto difuso al primer elemento xAen el universo X, de acuerdo con un orden dado, tal que
![]() .
.
Este criterio conlleva la dificultad de calcular un valor máximo de una
función real, precisamente A, definida sobre X.
Corte-a
Dado un conjunto difuso A en un universo X, sea ![]() un
número real positivo, pero estrictamente menor que 1. Diremos que el
número a es el umbral de corte. Elíjase un elemento
un
número real positivo, pero estrictamente menor que 1. Diremos que el
número a es el umbral de corte. Elíjase un elemento
![]() en el corte-a de A.
en el corte-a de A.
Centroide
Dado un conjunto difuso A en un universo X, sea
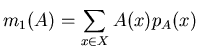 su centroide.
Elíjase al elemento
su centroide.
Elíjase al elemento ![]() tal que
tal que
Por ejemplo, con este criterio, cualquiera de los contribuyentes Azcárraga, Cárdenas, De la Madrid, Fox o Iglesias,
desdifusifica al conjunto de ``mayores'', y sólo Azcárraga
desdifusifica al de ``gigantes''.
De manera más general, para ![]() ,
se puede elegir al elemento
,
se puede elegir al elemento
![]() tal que
tal que
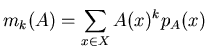 de A.
de A.
Centro de gravedad
Supongamos por ahora que el universo X posee una estructura geométrica
de espacio vectorial. Dados dos vectores
![]() se tiene definida
su suma, x1+x2, y para cada número real t se tiene también la
elongación t x1 del vector x1 por el escalar t. Para fijar
ideas, el lector puede suponer que X es el espacio tridimensional
se tiene definida
su suma, x1+x2, y para cada número real t se tiene también la
elongación t x1 del vector x1 por el escalar t. Para fijar
ideas, el lector puede suponer que X es el espacio tridimensional
![]() .
.
Dado un conjunto
![]() de n puntos en X, y dados ncoeficientes
de n puntos en X, y dados ncoeficientes
![]() tales que
tales que
![]() ,
el
vector
,
el
vector
![]() se dice ser una suma convexa de los
elementos de X' y está precisamente en el poliedro mínimo que
contiene a X'. Recíprocamente, se tiene que dado cualquier punto xen ese poliedro mínimo han de existir coeficientes
se dice ser una suma convexa de los
elementos de X' y está precisamente en el poliedro mínimo que
contiene a X'. Recíprocamente, se tiene que dado cualquier punto xen ese poliedro mínimo han de existir coeficientes
![]() tales que
tales que
![]() y
y
![]() .
Por esta razón a ese poliedro mínimo se le llama la cerradura convexa de X'.
.
Por esta razón a ese poliedro mínimo se le llama la cerradura convexa de X'.
Un conjunto difuso A en X se dice ser convexo si para
cualesquiera n puntos
![]() y cualesquiera ncoeficientes
y cualesquiera ncoeficientes
![]() tales que
tales que
![]() ,
se
tiene
,
se
tiene
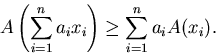
Sea ![]() .
Recordamos que el corte-a cerrado Aa de A consta
de todos los puntos cuyo grado de pertenencia a A no es inferior al
valor a. El centro de gravedad de altura a de A es
.
Recordamos que el corte-a cerrado Aa de A consta
de todos los puntos cuyo grado de pertenencia a A no es inferior al
valor a. El centro de gravedad de altura a de A es
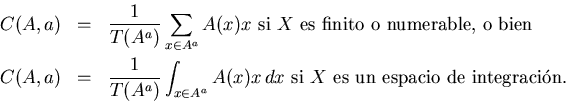
El centro de gravedad C(A,a) es pues el promedio de los elementos en el corte-a de A.
El centro de gravedad básico es el centro de gravedad de altura 0.
El centro de gravedad máximo es el centro de gravedad de altura
![]() .
.
En el caso de que A sea un conjunto convexo, cualquiera de los centros básico o máximo puede ser un buen representante del conjunto difuso A.
Sin embargo, si A no es convexo, la selección por centros puede ser
muy desafortunada. Por ejemplo, si A fuese un conjunto usual, entonces
se podría elegir a un elemento fuera de A con este criterio.
Ejemplo. Sea X=[0,1] y sea Ap el conjunto difuso
![]() ,
con p>0. Para p=2 la gráfica de Ap es una
parábola. Para
,
con p>0. Para p=2 la gráfica de Ap es una
parábola. Para
![]() ,
coincide con la gráfica de la raíz
cuadrada según se muestra en la figura 4.
,
coincide con la gráfica de la raíz
cuadrada según se muestra en la figura 4.
Si ![]() ,
el conjunto Ap es convexo.
,
el conjunto Ap es convexo.
Dado ![]() se tiene:
se tiene:
![]() .
Por tanto, el corte-a cerrado es
.
Por tanto, el corte-a cerrado es
![]() .
Así pues, el tamaño de
este corte-a es
.
Así pues, el tamaño de
este corte-a es
![]() y,
un cálculo directo muestra que
y,
un cálculo directo muestra que
Para ![]() ,
el conjunto Ap es convexo. Por lo cual, el grado de
pertenencia del centro no será inferior al promedio de los grados de
pertenencia. En este caso, de la ec. (4) se ve que cuando
,
el conjunto Ap es convexo. Por lo cual, el grado de
pertenencia del centro no será inferior al promedio de los grados de
pertenencia. En este caso, de la ec. (4) se ve que cuando
![]() ,
es decir, cuando p decrece hacia cero, entonces
independientemente del umbral
,
es decir, cuando p decrece hacia cero, entonces
independientemente del umbral ![]() el centro tenderá a ser
el centro tenderá a ser
![]() ,
es decir, el centro de gravedad tenderá a ser el punto
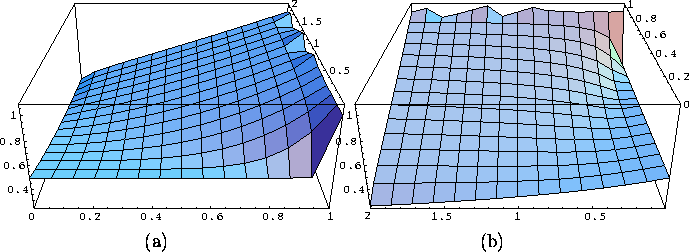
medio del universo. Véase esto en la figura 7 (a), donde se ve
la gráfica de centros de gravedad, rotada de manera que en un
primer plano aparezca el correspondiente a p=0, y la escala de valores de
la altura a.
,
es decir, el centro de gravedad tenderá a ser el punto
medio del universo. Véase esto en la figura 7 (a), donde se ve
la gráfica de centros de gravedad, rotada de manera que en un
primer plano aparezca el correspondiente a p=0, y la escala de valores de
la altura a.
 |
Para p> 1, el conjunto Ap no es convexo. En particular, si p fuese
un entero, de la ec. (4) resulta