


Siguiente: Derivadas covariantes
Arriba: Geometría Diferencial y Relatividad
Anterior: Longitudes
Sea 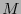 un espacio topológico separado. Un mapa es una pareja
un espacio topológico separado. Un mapa es una pareja 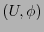 donde
donde 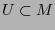 es un conjunto abierto no-vacío y
es un conjunto abierto no-vacío y
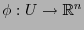 es un homeomorfismo
es un homeomorfismo
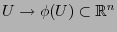 , del cual se dice que determina un sistemas de coordenadas en
, del cual se dice que determina un sistemas de coordenadas en 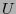 . Un atlas es una colección de mapas
. Un atlas es una colección de mapas
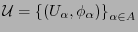 con las propiededes siguientes:
con las propiededes siguientes:
-
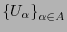 es un recubrimiento de
es un recubrimiento de 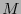 :
:
 .
.
- Los mapas son compatibles en intersecciones:
Si los homomorfismos son de clase  , el atlas se dice de clase
, el atlas se dice de clase  .
.
La pareja 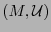 , donde
, donde  es un atlas maximal de clase
es un atlas maximal de clase  se dice ser una
se dice ser una  -variedad (diferenciable de orden
-variedad (diferenciable de orden 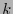 ), de dimensión
), de dimensión 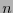 .
.
Aunque los mapas determinan inclusiones locales en 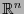 , se tiene:
, se tiene:
Como ejemplos de variedades están las siguientes:
- El espacio euclidiano
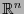 es una
es una 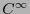 -variedad de dimensión
-variedad de dimensión 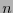 .
.
- Esfera
-
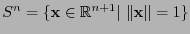 (los hemisferios determinan mapas, o bien las proyecciones estereográficas suprimiendo ``polos'').
(los hemisferios determinan mapas, o bien las proyecciones estereográficas suprimiendo ``polos'').
- Toro
-
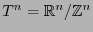 (los mapas son relativos a la topología cociente).
(los mapas son relativos a la topología cociente).
- Superficies de Riemann de diverso género
- Así como el toro bidimensional
 tiene un hoyo (es una dona) una superficie de Riemann de género
tiene un hoyo (es una dona) una superficie de Riemann de género  es una superficie con
es una superficie con  hoyos.
hoyos.
- Grupos de Lie
- Sea
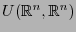 el grupo de automorfismos lineales
el grupo de automorfismos lineales
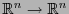 . Entonces
. Entonces
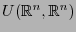 es un espacio topológico, de hecho metrizable con la norma espectral, por ejemplo, y es además un grupo. Un grupo de Lie es un grupo topológico dotado de una estructura de variedad.
es un espacio topológico, de hecho metrizable con la norma espectral, por ejemplo, y es además un grupo. Un grupo de Lie es un grupo topológico dotado de una estructura de variedad.
- Productos de variedades
- Si
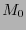 y
y 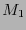 son variedades, su producto
son variedades, su producto  puede ser dotado de una estructura de variedad.
puede ser dotado de una estructura de variedad.
Una función
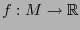 es de clase
es de clase  si para cada punto
si para cada punto 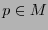 y mapa
y mapa 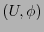 que contenga a
que contenga a  , se tiene que
, se tiene que
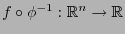 es de clase
es de clase  en una vecindad abierta de
en una vecindad abierta de 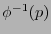 . Sea
. Sea 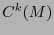 la colección de funciones
la colección de funciones
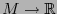 de clase
de clase  . Claramente,
. Claramente, 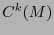 es un espacio vectorial real.
es un espacio vectorial real.
En cada punto 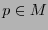 , supongamos que
, supongamos que
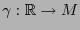 es una curva en
es una curva en 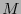 tal que pasa por
tal que pasa por  , digamos
, digamos 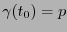 . Consideremos la transformación
. Consideremos la transformación
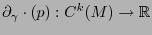 definida como
definida como
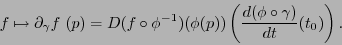 |
(6.1) |
Puede verse que
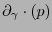 es independiente de
es independiente de  y es lineal sobre
y es lineal sobre 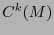 , así pues, es un funcional lineal y es un elemento del espacio dual
, así pues, es un funcional lineal y es un elemento del espacio dual
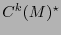 . Esta transformación es la derivada direccional en
. Esta transformación es la derivada direccional en  según la curva
según la curva 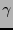 . Sea
. Sea
 la colección de derivadas direccionales sobre curvas que pasen por
la colección de derivadas direccionales sobre curvas que pasen por 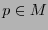 . La familia
. La familia 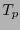 es un espacio vectorial real y se llama espacio tangente a
es un espacio vectorial real y se llama espacio tangente a 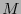 en
en 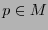 .
.
Escribiendo
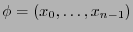 , usando la regla de la cadena, se tiene de la expresión (6.1):
, usando la regla de la cadena, se tiene de la expresión (6.1):
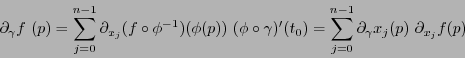 |
(6.2) |
así pues, la derivada direccional en  se expresa como una combinación lineal de las derivadas parciales
se expresa como una combinación lineal de las derivadas parciales
 . Se tiene pues que la colección de funcionales
. Se tiene pues que la colección de funcionales
 es una base de
es una base de 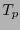 , llamada de coordenadas, y por tanto
, llamada de coordenadas, y por tanto 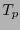 es de dimensión
es de dimensión 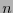 .
.
Ahora bien, si se cambia de coordenadas en el mapa, digamos a
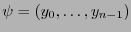 , entonces por (6.2):
, entonces por (6.2):
En consecuencia para todo
 :
:
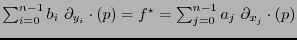 si y sólo si:
si y sólo si:
Se ha de tener entonces
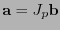 , donde
, donde
![$J_p=\left[\partial_{y_i}x_j(p)\right]_{0\leq i,j\leq n-1}$](img392.png) es la llamada matriz jacobiana del cambio del sistema de coordenadas. Por el Teorema de la Función Inversa:
es la llamada matriz jacobiana del cambio del sistema de coordenadas. Por el Teorema de la Función Inversa:
![\begin{displaymath}
{\bf b} = J_p^{-1}{\bf a}\ \ \mbox{ donde }\ \ J_p^{-1}=\left[\partial_{x_j}y_i(p)\right]_{0\leq i,j\leq n-1}
\end{displaymath}](img393.png) |
(6.3) |
El espacio cotangente en el punto 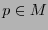 es el dual
es el dual 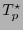 del espacio tangente
del espacio tangente 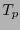 .
.
Por ejemplo, si 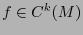 es una función, el funcional
es una función, el funcional
es un elemento del espacio cotangente 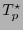 .
. 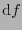 se dice ser el gradiente de
se dice ser el gradiente de 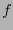 en
en  .
.
Si
 es un mapa en
es un mapa en  , entonces
, entonces
por tanto
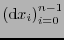 es la base de
es la base de 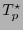 dual de la base de coordenadas
dual de la base de coordenadas
 de
de 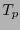 .
.
Los vectores tangentes son 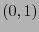 -tensores y los funcionales son
-tensores y los funcionales son  -tensores. En general el espacio de los
-tensores. En general el espacio de los  -tensores tiene como base
-tensores tiene como base
Por tanto, todo  -tensor puede escribirse de la forma
-tensor puede escribirse de la forma
Si se cambia de coordenadas en el mapa, digamos a
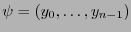 , entonces respecto a las bases
, entonces respecto a las bases
 ,
,
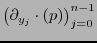 y a sus duales
y a sus duales
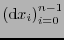 ,
,
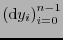 , el cambio de coordenadas del
, el cambio de coordenadas del  -tensor se hace según (6.3), (2.1), (2.4) y (3.3).
-tensor se hace según (6.3), (2.1), (2.4) y (3.3).
Sea
![$G=\left[g_{ij}\right]_{i,j\in[\![0,n-1]\!]}$](img405.png) una matriz simétrica no-singular.
una matriz simétrica no-singular.  determina un
determina un 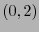 -tensor
-tensor
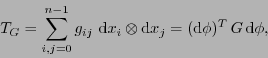 |
(6.4) |
el cual se dice ser una métrica. La raíz cuadrada de éste es el elemento de superficie:
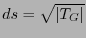 .
.
Si se tiene un nuevo sistema de coordenadas
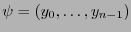 en un punto
en un punto 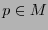 , de acuerdo con las fórmulas de cambio de variables,
, de acuerdo con las fórmulas de cambio de variables,
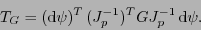 |
(6.5) |
Por ejemplo, para 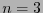 , la matriz
, la matriz  determina el elemento de superficie
determina el elemento de superficie
Al hacer el cambio a coordenadas esféricas:
(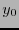 es el radio,
es el radio, 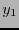 es el ángulo cenital e
es el ángulo cenital e 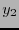 es el ángulo azimutal), se tiene que el elemento de superficie se expresa como
es el ángulo azimutal), se tiene que el elemento de superficie se expresa como
Las matrices semiunitarias (reales) son aquellas con valores propios 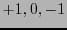 . Al ser diagonalizadas adquieren la forma
. Al ser diagonalizadas adquieren la forma
![$G=\mbox{diag}[+1 \ \ \cdots \ \ +1 \ \ -1 \ \ \cdots \ \ -1 \ \ 0 \ \ \cdots \ \ 0]$](img417.png) (llamada forma canónica). Si
(llamada forma canónica). Si 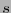 es la multiplicidad de
es la multiplicidad de 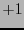 y
y 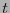 la de
la de 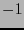 , entonces
, entonces  es la signatura y
es la signatura y 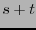 el rango de
el rango de  . Si
. Si 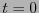 ,
,  se dice ser euclidiana o positiva. La matriz es pues una métrica si su rango es
se dice ser euclidiana o positiva. La matriz es pues una métrica si su rango es 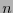 . Una métrica euclidiana es positiva definida. Si
. Una métrica euclidiana es positiva definida. Si 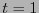 (es decir la multiplicidad de
(es decir la multiplicidad de 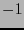 es
es 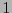 ), la métrica se dice ser lorentziana. En relatividad, en particular en el espacio-tiempo, las métricas lorentzianas son de gran relevancia.
), la métrica se dice ser lorentziana. En relatividad, en particular en el espacio-tiempo, las métricas lorentzianas son de gran relevancia.
 , donde
, donde  es una métrica euclidiana, se dice ser el espacio plano.
es una métrica euclidiana, se dice ser el espacio plano.
 , donde
, donde  es una métrica lorentziana, se dice ser un espacio curvo.
es una métrica lorentziana, se dice ser un espacio curvo.
Sea 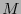 una
una  -variedad diferenciable de dimensión
-variedad diferenciable de dimensión 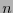 . Sea
. Sea
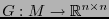 un campo que a cada punto
un campo que a cada punto 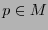 le asocia una métrica en el espacio tangente
le asocia una métrica en el espacio tangente 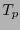 . Puede verse que en cada punto
. Puede verse que en cada punto 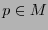 existe un sistema de coordenadas
existe un sistema de coordenadas
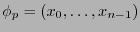 tal que
tal que 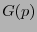 queda en forma canónica, las primeras derivadas
queda en forma canónica, las primeras derivadas
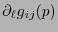 se anulan todas pero las segundas derivadas
se anulan todas pero las segundas derivadas
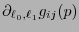 no se anulan todas. Tal sistema
no se anulan todas. Tal sistema 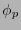 se dice ser un sistema riemanniano normal o bien un marco local lorentziano. La existencia de sistemas riemannianos normales se prueba considerando las fórmulas de cambios de base, expansiones de Taylor y cambios de orientación mediante el tensor de Levi-Civitá [2].
se dice ser un sistema riemanniano normal o bien un marco local lorentziano. La existencia de sistemas riemannianos normales se prueba considerando las fórmulas de cambios de base, expansiones de Taylor y cambios de orientación mediante el tensor de Levi-Civitá [2].
Precisamente al considerar el tensor de Levi-Civitá
![$\left(\varepsilon_{\bf i}\right)_{{\bf i}\in[\![0,n-1]\!]^n}$](img433.png) (
(
 si
si  es una permutación y
es una permutación y
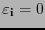 en otro caso) se tiene que cualquiera que sea la matriz
en otro caso) se tiene que cualquiera que sea la matriz
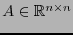 :
:
En particular, si se tiene un nuevo sistema de coordenadas
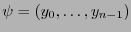 en un punto
en un punto 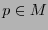 se tiene
se tiene
Por tanto
![\begin{displaymath}
\forall{\bf i}\in[\![0,n-1]\!]^n:\ \ \varepsilon_{\bf i} = (...
...\varepsilon_{\bf j}\prod_{k=0}^{n-1}\partial_{y_{i_k}}x_{j_k},
\end{displaymath}](img439.png) |
(6.6) |
es decir, el tensor de Levi-Civitá se afecta por un factor
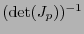 con el cambio de base.
con el cambio de base.
Ahora bien, si  es una métrica, de acuerdo con la relación (6.5), se tiene
es una métrica, de acuerdo con la relación (6.5), se tiene
donde 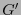 es la matriz que representa a la métrica respecto al nuevo sistema de coordenadas.
es la matriz que representa a la métrica respecto al nuevo sistema de coordenadas.



Siguiente: Derivadas covariantes
Arriba: Geometría Diferencial y Relatividad
Anterior: Longitudes
Guillermo M. Luna
2011-01-03
![]() un espacio topológico separado. Un mapa es una pareja
un espacio topológico separado. Un mapa es una pareja ![]() donde
donde ![]() es un conjunto abierto no-vacío y
es un conjunto abierto no-vacío y
![]() es un homeomorfismo
es un homeomorfismo
![]() , del cual se dice que determina un sistemas de coordenadas en
, del cual se dice que determina un sistemas de coordenadas en ![]() . Un atlas es una colección de mapas
. Un atlas es una colección de mapas
![]() con las propiededes siguientes:
con las propiededes siguientes:
![]() , donde
, donde ![]() es un atlas maximal de clase
es un atlas maximal de clase ![]() se dice ser una
se dice ser una ![]() -variedad (diferenciable de orden
-variedad (diferenciable de orden ![]() ), de dimensión
), de dimensión ![]() .
.
![]() , se tiene:
, se tiene:
![]() es de clase
es de clase ![]() si para cada punto
si para cada punto ![]() y mapa
y mapa ![]() que contenga a
que contenga a ![]() , se tiene que
, se tiene que
![]() es de clase
es de clase ![]() en una vecindad abierta de
en una vecindad abierta de ![]() . Sea
. Sea ![]() la colección de funciones
la colección de funciones
![]() de clase
de clase ![]() . Claramente,
. Claramente, ![]() es un espacio vectorial real.
es un espacio vectorial real.
![]() , supongamos que
, supongamos que
![]() es una curva en
es una curva en ![]() tal que pasa por
tal que pasa por ![]() , digamos
, digamos ![]() . Consideremos la transformación
. Consideremos la transformación
![]() definida como
definida como
![]() , usando la regla de la cadena, se tiene de la expresión (6.1):
, usando la regla de la cadena, se tiene de la expresión (6.1):
![]() , entonces por (6.2):
, entonces por (6.2):
![\begin{displaymath}\forall i\in[\![0,n-1]\!]:\ \partial_{y_i}f(p) = \sum_{j=0}^{n-1}\partial_{y_i}x_j(p)\ \partial_{x_j}f(p).\end{displaymath}](img387.png)

![]() es el dual
es el dual ![]() del espacio tangente
del espacio tangente ![]() .
.
![]() es una función, el funcional
es una función, el funcional
![]() es un mapa en
es un mapa en ![]() , entonces
, entonces
![]() -tensores y los funcionales son
-tensores y los funcionales son ![]() -tensores. En general el espacio de los
-tensores. En general el espacio de los ![]() -tensores tiene como base
-tensores tiene como base
![]() una matriz simétrica no-singular.
una matriz simétrica no-singular. ![]() determina un
determina un ![]() -tensor
-tensor
![]() en un punto
en un punto ![]() , de acuerdo con las fórmulas de cambio de variables,
, de acuerdo con las fórmulas de cambio de variables,
![]() , la matriz
, la matriz ![]() determina el elemento de superficie
determina el elemento de superficie
![]() una
una ![]() -variedad diferenciable de dimensión
-variedad diferenciable de dimensión ![]() . Sea
. Sea
![]() un campo que a cada punto
un campo que a cada punto ![]() le asocia una métrica en el espacio tangente
le asocia una métrica en el espacio tangente ![]() . Puede verse que en cada punto
. Puede verse que en cada punto ![]() existe un sistema de coordenadas
existe un sistema de coordenadas
![]() tal que
tal que ![]() queda en forma canónica, las primeras derivadas
queda en forma canónica, las primeras derivadas
![]() se anulan todas pero las segundas derivadas
se anulan todas pero las segundas derivadas
![]() no se anulan todas. Tal sistema
no se anulan todas. Tal sistema ![]() se dice ser un sistema riemanniano normal o bien un marco local lorentziano. La existencia de sistemas riemannianos normales se prueba considerando las fórmulas de cambios de base, expansiones de Taylor y cambios de orientación mediante el tensor de Levi-Civitá [2].
se dice ser un sistema riemanniano normal o bien un marco local lorentziano. La existencia de sistemas riemannianos normales se prueba considerando las fórmulas de cambios de base, expansiones de Taylor y cambios de orientación mediante el tensor de Levi-Civitá [2].
![]() (
(
![]() si
si ![]() es una permutación y
es una permutación y
![]() en otro caso) se tiene que cualquiera que sea la matriz
en otro caso) se tiene que cualquiera que sea la matriz
![]() :
:
![\begin{displaymath}\forall{\bf i}\in[\![0,n-1]\!]^n:\ \ \varepsilon_{\bf i}\det(...
...{{\bf j}\in S_n}\varepsilon_{\bf j}\prod_{k=0}^{n-1}a_{i_kj_k}.\end{displaymath}](img437.png)
![\begin{displaymath}\forall{\bf i}\in[\![0,n-1]\!]^n:\ \ \varepsilon_{\bf i}\det(...
...}\varepsilon_{\bf j}\prod_{k=0}^{n-1}\partial_{y_{i_k}}x_{j_k}.\end{displaymath}](img438.png)
![]() es una métrica, de acuerdo con la relación (6.5), se tiene
es una métrica, de acuerdo con la relación (6.5), se tiene