Siguiente: Conmutadores y desviaciones geodésicas Arriba: Curvatura Anterior: Curvatura

Ejemplo: La esfera $S^2$

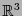En $\mathbb{R}^3$ consideremos la esfera 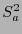$S^2_a$ de radio $a\in\mathbb{R}^+$,

$$S^2_a=\{{\bf x}\in\mathbb{R}^3\vert\ x_0^2+x_1^2+x_2^2 = a^2\}.$$

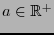Una parametrización de la esfera está dada por las coordenadas esféricas en términos de los ángulos cenital y azimutal

$$x_0 = a \,\mbox{\rm sen}\,\theta_0\cos \theta_1\ \ ,\ \ x_1 =... ...heta_0\,\mbox{\rm sen}\,\theta_1\ \ ,\ \ x_2 = a \cos \theta_0.$$

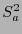$S^2_a$ es pues una 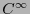$C^{\infty}$-variedad de dimensión 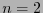$n=2$. El elemento de superficie, o métrica, satisface:

$$(ds)^2=a^2((\mbox{d}\theta_0)^2 + \,\mbox{\rm sen}\,^2\theta_... ...rray}{c} \mbox{d}\theta_0\\ \mbox{d}\theta_1 \end{array}\right]$$

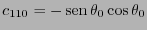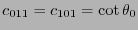Atendiendo a las relaciones (7.3) se tiene, por ejemplo, $c_{110} = -\,\mbox{\rm sen}\,\theta_0\cos\theta_0$ y $c_{011} = c_{101} = \cot\theta_0$. Por tanto, de la relación (10.2) se ha de tener

$$\begin{eqnarray*} r_{0,101} &=& \nabla_0c_{110} - \nabla_{1}c_{010} + \sum_{j_1=... ...s\theta_0\ \cot\theta_0)] \\ &=& \,\mbox{\rm sen}\,^2\theta_0. \end{eqnarray*}$$

Entonces, de (10.5), 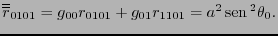$\overline{\overline{r}}_{0101} = g_{00}r_{0101} + g_{01}r_{1101} = a^2\,\mbox{\rm sen}\,^2\theta_0.$ De hecho todas las componentes del tensor de Riemann o bien se anulan, o bien coinciden con 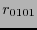$r_{0101}$ (salvo un signo). El tensor de Ricci, tiene componentes, de acuerdo con (10.8),

$$S = \left[\begin{array}{cc} 1 & 0 \\ 0 & \,\mbox{\rm sen}\,^2\theta_0 \\ \end{array}\right].$$

Por tanto, el escalar de Ricci es 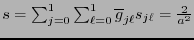$s= \sum_{j=0}^{1} \sum_{\ell=0}^{1}\overline{g}_{j\ell}s_{j\ell} = \frac{2}{a^2}$, y es positivo y constante en la esfera. Esto da cuenta, precisamente, de la regularidad de la esfera. $\Box$