


Siguiente: Ejemplo: La esfera
Arriba: Geometría Diferencial y Relatividad
Anterior: Geodésicas
Sea 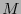 una
una  -variedad y sea
-variedad y sea 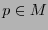 un punto en ella. Sea
un punto en ella. Sea 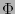 la aplicación descrita al final de la sección anterior que identifica al espacio tangente
la aplicación descrita al final de la sección anterior que identifica al espacio tangente 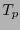 con una vecindad de
con una vecindad de  . Dados dos vectores
. Dados dos vectores
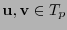 , consideremos el ``paralelogramo'' con aristas paralelas a los vectores
, consideremos el ``paralelogramo'' con aristas paralelas a los vectores
 , cuyas longitudes están dadas por una razón
, cuyas longitudes están dadas por una razón 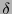 , y hagamos que un vector
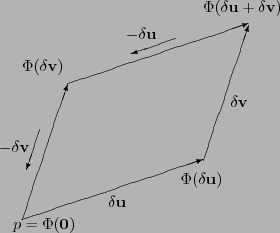
, y hagamos que un vector 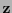 se transporte de manera paralela a lo largo de su perímetro en un sentido antihorario (véase la figura 1.1)
se transporte de manera paralela a lo largo de su perímetro en un sentido antihorario (véase la figura 1.1)
Figura 1.1:
Transporte paralelo en un paralelogramo.
 |
Cuando 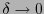 , la posición final del vector
, la posición final del vector 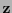 se puede poner como un vector, es decir un
se puede poner como un vector, es decir un  -tensor, cuyas componentes son propiamente
-tensor, cuyas componentes son propiamente  -tensores, es decir
-tensores, es decir
![\begin{displaymath}
{\bf z}_{\mbox{\scriptsize fin}} = \overline{R}({\bf z},d{\b...
...ell\in[\![0,n-1]\!]} r_{i,jk\ell}\,z_j\,du_k\,dv_{\ell}\,dx_i.
\end{displaymath}](img523.png) |
(10.1) |
Como el transporte es paralelo debe satisfacerse la ecuación de transporte paralelo (8.2), y por tanto
![\begin{displaymath}
\forall i,j,k,\ell\in[\![0,n-1]\!]:\ \ r_{i,jk\ell} = \nabla...
...ft[c_{j_1,ki}c_{j,\ell j_1} - c_{j_1,\ell i}c_{j,kj_1}\right].
\end{displaymath}](img524.png) |
(10.2) |
El 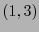 -tensor
-tensor
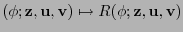 cuyas componentes están dadas por (10.2) se llama el tensor de Riemann. De (10.2) se ve inmediatamente que el tensor
cuyas componentes están dadas por (10.2) se llama el tensor de Riemann. De (10.2) se ve inmediatamente que el tensor  es alternante respecto a sus dos últimos argumentos:
es alternante respecto a sus dos últimos argumentos:
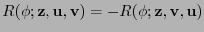 (en la figura 1.1 se ve que intercambiar esos argumentos es equivalente a intercambiar el sentido del recorrido en el perímetro del paralelogramo). Si
(en la figura 1.1 se ve que intercambiar esos argumentos es equivalente a intercambiar el sentido del recorrido en el perímetro del paralelogramo). Si  es idénticamente cero, entonces la variedad
es idénticamente cero, entonces la variedad 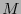 se dice ser plana.
se dice ser plana.
El tensor de torsión es de orden 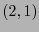 y tiene como componentes
y tiene como componentes
![\begin{displaymath}
\forall i,j,k\in[\![0,n-1]\!]:\ \tau_{ij,k} = c_{i,jk} - c_{j,ik}.
\end{displaymath}](img530.png) |
(10.3) |
Por otro lado, puede verse que las derivadas covariantes pueden dejar de ser conmutativas:
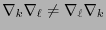 . De hecho, puede verse que el conmutador de tales derivadas está dado por el tensor de Riemann y el de torsión:
. De hecho, puede verse que el conmutador de tales derivadas está dado por el tensor de Riemann y el de torsión:
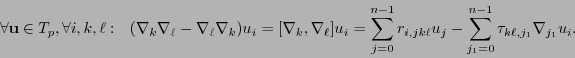 |
(10.4) |
El tensor de Riemann también puede presentarse como un 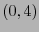 -tensor definiendo como nuevas componentes
-tensor definiendo como nuevas componentes
![\begin{displaymath}
\forall i,j,k,\ell\in[\![0,n-1]\!]:\ \ \overline{\overline{r}}_{ijk\ell} = \sum_{i_1=0}^{n-1}g_{ii_1}r_{i_1,jk\ell}
\end{displaymath}](img533.png) |
(10.5) |
donde
 es el tensor que define la métrica.
Puede verse que valen las siguientes relaciones de simetría y alternancia:
es el tensor que define la métrica.
Puede verse que valen las siguientes relaciones de simetría y alternancia:
![\begin{displaymath}
\forall i,j,k,\ell\in[\![0,n-1]\!]:\ \ \left\{\begin{array}{...
...} + \overline{\overline{r}}_{i\ell jk} = 0
\end{array}\right.
\end{displaymath}](img535.png) |
(10.6) |
Calculando las derivadas covariantes de las componentes del tensor de Riemann se comprueba que valen las identidades de Bianchi:
![\begin{displaymath}
\forall i,j,k,\ell,m\in[\![0,n-1]\!]:\ \ \nabla_mr_{i,jk\ell} + \nabla_kr_{i,j\ell m} + \nabla_{\ell}r_{i,jmk} = 0
\end{displaymath}](img536.png) |
(10.7) |
(obsérvese que se aplica una rotación a los tres últimos índices 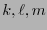 ). Las identidades de Bianchi son muy similares a las identidades de Jacobi:
). Las identidades de Bianchi son muy similares a las identidades de Jacobi:
donde
![$[\nabla_m,\nabla_k]=\nabla_m\,\nabla_k - \nabla_k\,\nabla_m$](img539.png) es el conmutador de las derivadas covariantes.
es el conmutador de las derivadas covariantes.
El tensor de Ricci es el 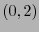 -tensor con componentes
-tensor con componentes
![\begin{displaymath}
\forall j,\ell\in[\![0,n-1]\!]:\ \ s_{j\ell} = \sum_{i=0}^{n-1}r_{i,ji\ell}.
\end{displaymath}](img540.png) |
(10.8) |
Así pues, de acuerdo con la relación (3.4) el tensor de Ricci es la contracción del de Riemann respecto a los índices 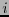 y
y 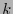 .
Por las relaciones de simetría y alternancia (10.6) se tiene
.
Por las relaciones de simetría y alternancia (10.6) se tiene
Por las mismas relaciones (10.6), cualquier otra contracción del de Riemann o bien se anula o bien coincide con el tensor de Ricci salvo por un signo. Por tanto, el de Ricci es esencialmente la única contracción del de Riemann.
Si
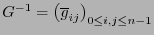 es la inversa de la matriz
es la inversa de la matriz  de componentes del tensor que define la métrica, entonces el escalar de Ricci es
de componentes del tensor que define la métrica, entonces el escalar de Ricci es
 . La curvatura de la variedad está definida como este escalar.
. La curvatura de la variedad está definida como este escalar.
Al realizar una doble contracción a las identidades de Bianchi (10.7) se tiene
![$\forall k\in[\![0,n-1]\!]$](img544.png) :
:
o sea
![\begin{displaymath}
\sum_{i\in[\![0,n-1]\!]} \nabla_is_{ik} = \frac{1}{2} \nabla_k s.
\end{displaymath}](img546.png) |
(10.9) |
El  -tensor
-tensor  con componentes
con componentes
se llama tensor de Einstein. Claramente, las identidades contraídas de Bianchi (10.9) son equivalentes a
Subsections



Siguiente: Ejemplo: La esfera
Arriba: Geometría Diferencial y Relatividad
Anterior: Geodésicas
Guillermo M. Luna
2011-01-03
![]() una
una ![]() -variedad y sea
-variedad y sea ![]() un punto en ella. Sea
un punto en ella. Sea ![]() la aplicación descrita al final de la sección anterior que identifica al espacio tangente
la aplicación descrita al final de la sección anterior que identifica al espacio tangente ![]() con una vecindad de
con una vecindad de ![]() . Dados dos vectores
. Dados dos vectores
![]() , consideremos el ``paralelogramo'' con aristas paralelas a los vectores
, consideremos el ``paralelogramo'' con aristas paralelas a los vectores
![]() , cuyas longitudes están dadas por una razón
, cuyas longitudes están dadas por una razón ![]() , y hagamos que un vector
, y hagamos que un vector ![]() se transporte de manera paralela a lo largo de su perímetro en un sentido antihorario (véase la figura 1.1)
se transporte de manera paralela a lo largo de su perímetro en un sentido antihorario (véase la figura 1.1)
![]() , la posición final del vector
, la posición final del vector ![]() se puede poner como un vector, es decir un
se puede poner como un vector, es decir un ![]() -tensor, cuyas componentes son propiamente
-tensor, cuyas componentes son propiamente ![]() -tensores, es decir
-tensores, es decir
![]() y tiene como componentes
y tiene como componentes
![]() . De hecho, puede verse que el conmutador de tales derivadas está dado por el tensor de Riemann y el de torsión:
. De hecho, puede verse que el conmutador de tales derivadas está dado por el tensor de Riemann y el de torsión:
![]() -tensor con componentes
-tensor con componentes
![]() es la inversa de la matriz
es la inversa de la matriz ![]() de componentes del tensor que define la métrica, entonces el escalar de Ricci es
de componentes del tensor que define la métrica, entonces el escalar de Ricci es
![]() . La curvatura de la variedad está definida como este escalar.
. La curvatura de la variedad está definida como este escalar.
![]() :
: