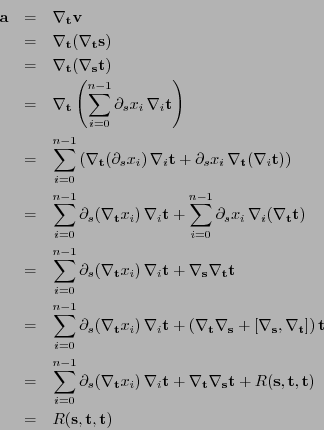Sea
![]() un vector de velocidad y sea
un vector de velocidad y sea
![]() uno de momento. Entonces, la energía está dada como
uno de momento. Entonces, la energía está dada como
![]() . Consideremos el
. Consideremos el ![]() -tensor
-tensor
![]() con componentes
con componentes
![]() Al considerar el
Al considerar el ![]() -tensor
-tensor ![]() con componentes
con componentes
![]() , se tiene
, se tiene
![]() . Por tanto
. Por tanto ![]() y
y ![]() tienen como arreglo de componentes a
tienen como arreglo de componentes a
![]() . Se tendrá entonces
. Se tendrá entonces
![]() , y ésta es una descomposición del momento
, y ésta es una descomposición del momento ![]() como una suma de una componente paralela a
como una suma de una componente paralela a ![]() y otra ortogonal a
y otra ortogonal a ![]() .
.
Sea
![]() la base canónica de
la base canónica de ![]() , que es ortonormal respecto a la métrica de Minkowski
, que es ortonormal respecto a la métrica de Minkowski
![]() . Sea
. Sea
![]() otra base ortonormal respecto a
otra base ortonormal respecto a ![]() tal que el cuarto vector
tal que el cuarto vector ![]() coincida con el cuarto de la base canónica
coincida con el cuarto de la base canónica ![]() . Entonces
. Entonces
![]() y los primeros tres vectores constituyen una base ortonormal en el espacio de tres dimensiones. La base
y los primeros tres vectores constituyen una base ortonormal en el espacio de tres dimensiones. La base ![]() es una cuarteta de observador. Sea
es una cuarteta de observador. Sea
![]() el sistema de coordenadas respecto a la base
el sistema de coordenadas respecto a la base ![]() . Entonces
. Entonces
![]() :
:
![]() . En consecuencia, el elemento de longitud es
. En consecuencia, el elemento de longitud es
![]() , y el de superficie es tal que
, y el de superficie es tal que
![]() . De acuerdo con la fórmula de cambio de bases (2.1), si
. De acuerdo con la fórmula de cambio de bases (2.1), si ![]() entonces
entonces
![]() ,
,
![]() donde
donde ![]() son las coordenadas respecto a
son las coordenadas respecto a ![]() . El producto escalar
. El producto escalar
![]() es independiente de las coordenadas:
es independiente de las coordenadas:
![]()
Generalizando la relación (10.4), para dos vectores
![]() definamos
definamos
De manera similar a (11.1), se define
Sea ![]() una
una ![]() -variedad de dimensión
-variedad de dimensión ![]() , con sistema de coordenadas
, con sistema de coordenadas
![]() , y sea
, y sea
![]() una familia de geodésicas tales que
una familia de geodésicas tales que
Por un lado, al ser ![]() y
y ![]() ortonormales,
ortonormales,
![]() . Supongamos que la torsión de
. Supongamos que la torsión de ![]() y
y ![]() es nula. De (11.3) se tiene
es nula. De (11.3) se tiene
![]() . Entonces:
. Entonces: