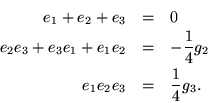Como ![]() tiene polos dobles en la clase residuo 0, la suma de
las dos clases residuo en la que toma algun valor es
cero. Esto también es consecuencia de que es una función par,
tiene polos dobles en la clase residuo 0, la suma de
las dos clases residuo en la que toma algun valor es
cero. Esto también es consecuencia de que es una función par,
![]() .
.
Si una clase residuo, en la cual
![]() ,
es
,
es
![]() donde
donde
![]() y
y
![]() ,
es decir
es un medio-periodo de
,
es decir
es un medio-periodo de ![]() ,
la otra clase residuo para el mismo
valor coincide con éste, es decir, cualquier punto de esta clase residuo es
un doble cero de
,
la otra clase residuo para el mismo
valor coincide con éste, es decir, cualquier punto de esta clase residuo es
un doble cero de ![]() ,
y un punto estacionario de
,
y un punto estacionario de ![]() ,
luego
también es un cero de
,
luego
también es un cero de ![]() .
.
Hay tres clases residuo de medios-periodos, llamados
![]() ,
donde
,
donde
![]() son cualquier
par de generadores de
son cualquier
par de generadores de ![]() ,
y
,
y
![]() ;
la unión de estas tres clases residuo con la clase residuo cero es la
red
;
la unión de estas tres clases residuo con la clase residuo cero es la
red ![]() .
Estas son las tres clases residuo de ceros de
.
Estas son las tres clases residuo de ceros de ![]() ,
que
como hemos visto es de orden 3, sus únicos polos son triples, en la
clase residuo cero.
,
que
como hemos visto es de orden 3, sus únicos polos son triples, en la
clase residuo cero.
Los valores estacionarios
![]() de
de ![]() son todos distintos.
Los valores estacionarios
e1,e2,e3,
son las raíces de la ecuación cúbica
4x3 - g2x-g3 = 0, ya
que de (2.1),
son todos distintos.
Los valores estacionarios
e1,e2,e3,
son las raíces de la ecuación cúbica
4x3 - g2x-g3 = 0, ya
que de (2.1), ![]() si y solo si
si y solo si ![]() es una raíz de
esta ecuación. Luego
es una raíz de
esta ecuación. Luego