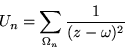


Next: Observaciones
Up: Análisis de una función.
Previous: Orden de las raíces
Sabemos que para que una serie sea convergente es condición necesaria y
suficiente que
para todo entero p>0 (ver referencia [7, pags. 222-223]).
Definiremos Un en términos de nuestra serie:
donde 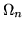 representa la suma de los n primeros paralelogramos
concéntricos a partir del origen. Así realizando las computaciones
pertinentes, tenemos que, si |z| < 1 :
representa la suma de los n primeros paralelogramos
concéntricos a partir del origen. Así realizando las computaciones
pertinentes, tenemos que, si |z| < 1 :
| 0 |
< |
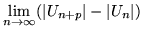 |
|
 |
< |
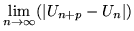 |
|
 |
= |
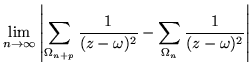 |
|
 |
= |
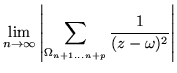 |
|
 |
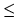 |
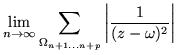 |
(3.4) |
 |
< |
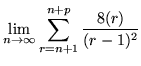 |
(3.5) |
 |
< |
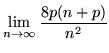 |
(3.6) |
 |
= |
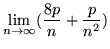 |
|
 |
= |
0 |
|
entonces
entonces
converge.
En la desigualdad de 3.4 a 3.5 la cota se da en términos de
(r-1)-2 para establecer las cotas máximas en cada uno de los
paralelogramos concéntricos. Y para obtener la siguiente desigualdad (eq.
3.6) se utilizó la menor de las cotas mayores, que es la que
corresponde al último paralelogramo (n+p).



Next: Observaciones
Up: Análisis de una función.
Previous: Orden de las raíces
Microcomputadoras
2001-03-09