Orden de las raíces

Realizando un análisis de la función, como en la sección 1.2; logramos la factorización de una raíz ^3.3. Y no sólo eso, sino que podemos apreciar el orden de ésta.

Primero se muestran la gráfica de contornos de valor absoluto de

$$\frac{\sum_{j= -\infty}^{\infty} \sum_{k= -\infty}^{\infty} \frac{1}{(z - j - ik)^2}} {(z-a)}$$

dado que nuestra raíz es de orden 2, gráficamente vemos que estamos anulando sólo un orden de la raíz, esto es, seguiremos teniendo una raíz en el punto a; pero ahora de orden 1.

En la gráfica siguiente anulamos por completo a la raíz.

  

Figure 3.11: Anulando un Orden de la Raíz.

  

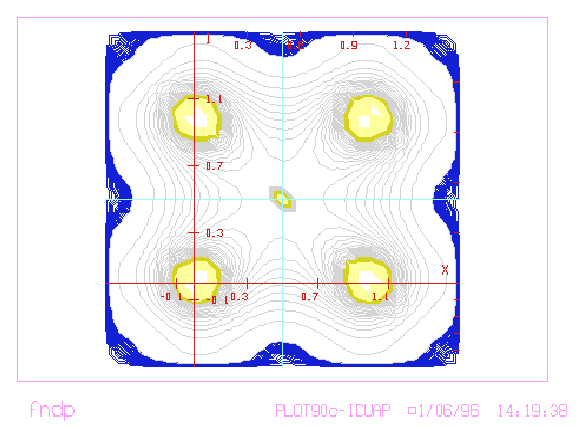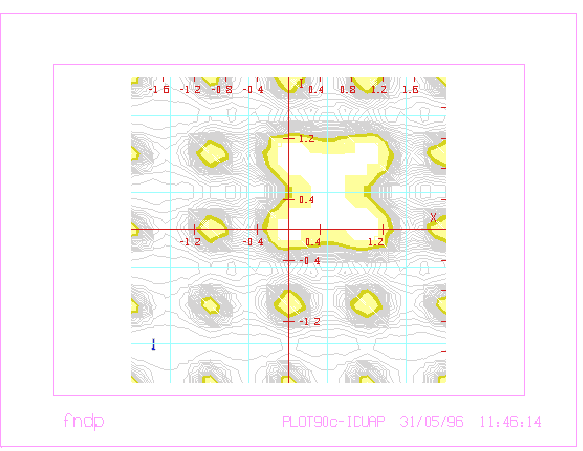
Figure 3.12: Anulando una Raíz.

Dado nuestros resultados anteriores, hemos mostrado que:

1.

La suma de los órdenes de los polos es igual a la suma de los órdenes de las raíces; este resultado es del teorema 8. De manera explícita, en cada paralelogramo-periódico tenemos en cero de orden 2 y un polo de orden 2.

2.

El orden de nuestra función es 2, aplicando la definición 15.