| w | = | 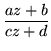 |
(73) |
Consider the basic linear fractional transformation
| w | = | 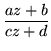 |
(73) |
| cwz + dw -az -b | = | 0. | (74) |
| c(wz)' + dw' -az' = | 0 | (75) | |
| c(wz)'' + dw'' -az'' = | 0 | (76) | |
| c(wz)''' + dw''' -az''' = | 0. | (77) |
![$\displaystyle \left[ \begin{array}{lll}
(wz)' & w' & -z' \\
(wz)'' & w'' & -z'...
...nd{array} \right]
\left[ \begin{array}{c} c \\ d \\ a \\ \end{array} \right]$](img119.gif) |
= | ![$\displaystyle \left[ \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right].$](img120.gif) |
(78) |
The determinant of this matrix, which is a Wronskian, must vanish to get a nontrivial solution. But
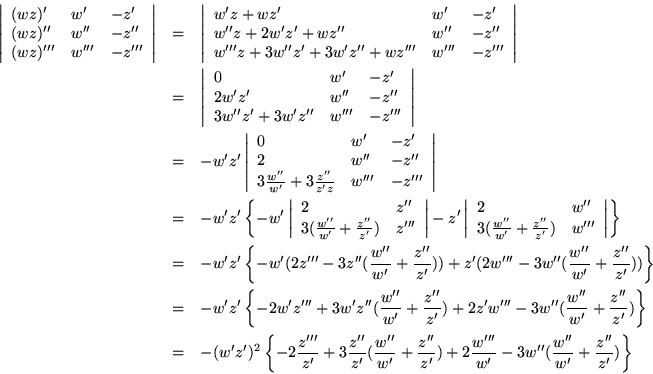
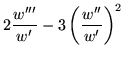 |
= | 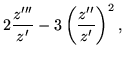 |
(79) |
| = | 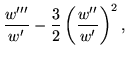 |
(80) | |
| = | 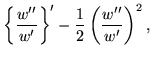 |
(81) | |
| = | ![$\displaystyle \frac{d^2}{dz^2}\left[\ln\frac{dw}{dz}\right]
-\frac{1}{2}\left\{\frac{d}{dz}\left[\ln\frac{dw}{dz}\right]\right\}^2.$](img129.gif) |
(82) |
The Schwartz derivative is not really a derivative (it is a differential invariant) because it doesn't follow the product rule when applied to products, nor does it even work linearly on sums, and it is furthermore immune to non-zero multiplicative constants. As the derivative was derived, w and z depended on a parameter with respect to which two differential expressions were identical. When z itself was the parameter, one result was obviously zero, forcing the other to assume the same value; which of the two was chosen creates an asymmetry by which
![]() .
.
Nevertheless, the invariant can be calculated for various w's all depending on the same z, for which the following rules and particular results can be verified through calculation:
The last three lines suggest the task of inverting the Schwartz derivative; that is, of finding w(z) for which
![]() ,
for some prescribed function Q. The answer is that one should solve the differential equation
,
for some prescribed function Q. The answer is that one should solve the differential equation
| (90) |
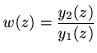 |
(91) |
For example, the conclusion in equation (87) follows from observing that a solution to
Given the privleged status of exponentials with respect to differentiation, we have already seen in equation (89) that
![]() ,
whereby complex exponentials generate constant Schwartz derivatives. How does this reconcile with the case where
,
whereby complex exponentials generate constant Schwartz derivatives. How does this reconcile with the case where
![]() where this might lead us to think that just constants have a zero Schwartz derivative?
where this might lead us to think that just constants have a zero Schwartz derivative?
Again we need to consider that the most general form of the solution of the associated Ricatti equation is a fractional linear combination of
![]() and
and
![]() .
But
.
But ![]() represents the confluent case where the two solutions are
represents the confluent case where the two solutions are
![]() and its derivative with respect to
and its derivative with respect to ![]() ,
namely
,
namely
![]() .
The limit gives a fractional linear combination of 1 and z, the Möbius transformation already seen.
.
The limit gives a fractional linear combination of 1 and z, the Möbius transformation already seen.
A somewhat similar discussion could be based on equation (88) where both n=1 and n=-1 give zero Schwartz derivatives, but it suffices to say that these two exceptions are already fractional linear transformations. Aside from that, the denominator of ![]() tends to zero with large z, so it is again possible to wonder about Schwartz derivatives which are small, but not necessarily zero.
tends to zero with large z, so it is again possible to wonder about Schwartz derivatives which are small, but not necessarily zero.
In turn it could be asked, what it means to have a mapping which is almost, but not quite, single valued? The example of the exponential shows that it could introduce a very long periodicity, with an anomaly which concentrates around infinity. Powers put a definitive multiple valuedness right at the origin, which of course extends right out to infinity. We could also ask, ``Can singlevaluedness be assured, at least in a finite region?'' It is a question which can be better answered later on.
That singlevaluedness is a delicate and unstable concept is already apparent in the implicit polynomial which was used to obtain its properties. At the level of polynomials, any addition whatsoever will create additional roots which may possibly be located far away, but whose vestiges could nevertheless be far reaching. Consider
![]() ,
for example. An extremely flat parabola has been added to a straight line which, although not changing the existing zero by much, introduces a new root near infinity.
,
for example. An extremely flat parabola has been added to a straight line which, although not changing the existing zero by much, introduces a new root near infinity.