Liouville's theorem: a bounded analytic function is constant

Suppose that |f(z)| < M and that Cauchy's integral formula is used to compare the values of f(z) at two points. Then

$$\frac{1}{2\pi i} \oint \left\{\frac{f(z)}{z-z_1} - \frac{f(z)}{z-z_2}\right\} dz.$$ f(z₂) - f(z₁) = 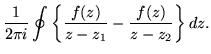(151)

A little rearrangement produces

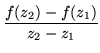$$\frac{f(z_2) - f(z_1)}{z_2-z_1} \frac{1}{2\pi i} \oint \frac{f(z)dz}{(z-z_0)^2} \left\{\frac{z-z_0}{z-z_1}\right\}\left\{\frac{z-z_0}{z-z_2} \right\},$$ = (152)

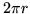which could very easily be used in an alternative derivation of the Cauchy formula for a derivative. Now, choose a huge circular contour centered on the auxiliary point z₀, and note that f(z) is still bounded however large the region. In Cauchy's formula the factor $1/(z-z_0) \approx 1/r$ gets the better of the situation and just compensates the $2\pi r$ in the arc length of the surrounding circle, but that just repeats what we already know, that the function is bounded.

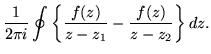
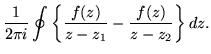
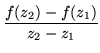
But in the difference we are calculating, the common denominator introduces an additional power of r, leaving little doubt that the combination $(M\times r)/r^2$ approaches zero. Very well, take the limit, and arrive at the conclusion a bounded analytic function can only be a constant. That is the content of Liouville's theorem.