To get some actual inequalities to work with, Cauchy's integral formula ought to be subjected to absolute values (depending on all four combinations arising from positive maxima and negative minima as found in the real as well as the imaginary part of the complex function), This is most conveniently done in polar coordinates. Let the contour be a circle of radius ![]() centered at the origin. Then, supposing that
centered at the origin. Then, supposing that
| = | (153) |
This series of inequalities relates the value of the function (as well as its derivatives) at the center of a circle of analyticity to the maximum value on the circumference of the circle. Any bound would establish an inequality, but the bound used in this series of equations is optimal, given that it actually occurs somewhere on the perimeter of the bounding circle.
But the inequality can be read in both directions, in the sense that there must be a place on the circumference where the absolute value of the function is greater than (or at least equal to) the absolute value of the function at the center. That is because the integral expresses an average of certain data, yet an average can never be strictly greater than all its data. But the more inclusive ``greater than or equal to'' could actually hold, supposing that all the data were equal.
Saying ``place'' rather than ``point'' is intended to invoke enough continuity to avoid sets of measure zero (like individual points) while evaluating the integral. Presumably the analyticity of f(z) provides this assurance.
Since the extreme case of equality in equation (155) reduces
![]() to the real constant
to the real constant ![]() ,
equations (157) through (159) and onwards experience the same reduction, establishing equality along the line.
,
equations (157) through (159) and onwards experience the same reduction, establishing equality along the line.
Supposing a Maclaurin series for f(z)
| f(z) | = | 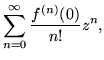 |
(160) |
| |f(z)| | 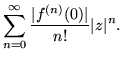 |
(161) |
| |f(z)| | 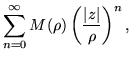 |
(162) | |
| (163) |
There are corresponding minimum inequalities, for functions which do not vanish within the circle; it is only necessary to apply the foregoing reasoning to the then finite-valued g(z)=1/f(z) in place of f(z).
For a single circle, these results are of limited utility, but it is easy enough to extend them to more general domains, as long as they accomodate the intermediate circles needed in the following argument. The main concern is with taking the bounding modulus from anywhere within the domain, rather than just from the boundary.
There are two possibilities. Suppose the greatest modulus sits at an interior point rather than on the boundary. Enclosing it within a circle small enough to still lie in the domain, we observe that there must be a point on the circumference of that little circle with a still greater modulus, which would be a contradiction, or all the values on that little circle would equal the purportedly greater modulus. So enlarge the circle until it makes contact with the boundary. If contact is made through the equality alternative, the contradiction consists in having a greater modulus than the one taken from the boundary (even though it isn't necessarily a circle any more).
The final result of all this reasoning is the maximum modulus principle, that the maximum absolute value of an analytic function lies on the boundary of any domain of analyticity.