| g(z) | = |  |
(164) |
Just as there are variants to Cauchy's integral formula yielding useful results, applying the bounds already obtained to more specific situations can give equally specific results. One idea is to examine the stability of a fixed point, which we know is influenced by its derivative. By translating and scaling, most functions can be made to vanish at zero with unit derivative; just introduce the new function
| g(z) | = |  |
(164) |
This preparation yields an analytic function vanishing at the origin, precluding the singularity of f(z)/z which would otherwise be found there. Again, relative to a circle of radius ![]() ,
,
| (165) | |||
| |f(z)| | 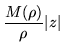 |
(166) | |
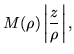 |
(167) |
| (168) |
The idea behind Schwartz's lemma can be followed in two directions. If zero is a superstable fixed point the maximum modulus inequality could be applied to f(z)/z2 get
| (169) | |||
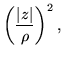 |
(170) |
The other direction would be to check for derivatives, which for an ordinary f with a fixed point at 0 would read
 |
(171) | ||
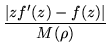 |
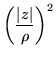 |
(172) |