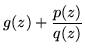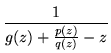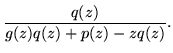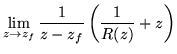Next: representation of a function
Up: Contour Integrals
Previous: Schwartz's lemma
Residues can show up in defining fixed points for rational functions. Suppose
that the function r,
| r(z) |
= |
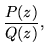 |
(173) |
is a quotient of two polynomials. If Q has lesser degree than P, division may be used to write
| r(z) |
= |
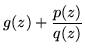 |
(174) |
wherein p and q have the desired property.
Consider a ``resolvent'' R(z) defined by
| R(z) |
= |
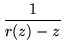 |
(175) |
which will have poles wherever r(z) has fixed points. As previously discussed, r(z)-z can be factored, allowing the writing of
| R(z) |
= |
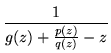 |
(176) |
| |
= |
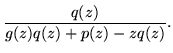 |
(177) |
This denominator has greater degree than the numerator, so it can be factored and R can be written as a sum of partial fractions (due allowance should be made for repeated factors)
| R(z) |
= |
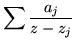 |
(178) |
for fixed points of r, namely zj. The aj's are residues of R, but we are interested in the stability of r(z).
| r(z) |
= |
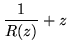 |
(179) |
| r'(zf) |
= |
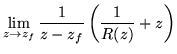 |
(180) |
| |
= |
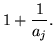 |
(181) |
So stability depends on negative (but not too negative) aj's.




Next: representation of a function
Up: Contour Integrals
Previous: Schwartz's lemma
Microcomputadoras
2001-04-05