However, to start from the beginning, consider the potential
![]() with the differential equation
with the differential equation
| = | 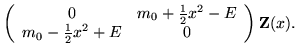 |
(8) |
Figure 1 shows both the phase plane solution and the wavefunction graphed as a function of the independent variable. This is done for two different values of the energy, with a mass on the order of 1.0 in the units to which the equation is normalized (which is about 1% of the mass of an electron in the real world).
Both graphs tend to be fairly cluttered, especially when several options are activated simultaneously. The first thing to do is to locate the classically forbidden region, where the total energy is less than the potential with the mass added, yet greater than the potential with the mass subtracted. The result is a coefficient matrix with equal signs on the two sides of the diagonal resulting in hyperbolic motion. Or in other words, the wave function varies exponentially in this region, either growing or diminishing. In the phase plane, the trajectory will either run outwards towards an asymptote or inwards toward the origin in a complementary direction.
The classically allowed region, in which the coefficient is sign antisymmetric and the solution elliptical rather than hyperbolic, is either where a positive total energy lies above the mass shell or a negative total energy lies below it. In these regions the solution point in the phase plane will rotate around the origin with a velocity corresponding to the amount of kinetic energy available.
In combination, one will see two spirals separated in radius by an amount corresponding to the forbidden region.
The graphs of the individual components follows the same behavior, oscillating is accessible regions and changing overall amplitude in the forbidden regions. The feature which distinguishes resonances from other solutions is that the ratio of inside amplitude to outside amplitude is greater than 1 and as large as possible within its local region. Conversely, an antiresonance is an energy value for which the ratio is reversed, and the amplitude within the well is minimal. The distinction between interior and exterior is one of what the potential is doing at infinity, compared to what it is like near the origin.