| = |  |
||
| = | ![$\displaystyle \left[\frac{1}{6}t^3-Et\right]_0^x$](img29.gif) |
||
| = | (9) |
Taking up the options offered by Equations 3 and 4
occasioned by seting the particle's mass to zero, the solution matrix for the massless Dirac harmonic oscillator would use the angle
| = |  |
||
| = | ![$\displaystyle \left[\frac{1}{6}t^3-Et\right]_0^x$](img29.gif) |
||
| = | (9) |
| = | 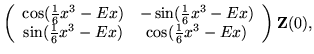 |
(10) |
When it comes time to include the mass in the solution, we need to work out the supplementary coefficient for ![]() which is
which is
![]() transformed by
transformed by ![]() .
Here
.
Here ![]() is the symmetric off-diagonal quaternion. Since it anticommutes with the antisymmetric off-diagonal
is the symmetric off-diagonal quaternion. Since it anticommutes with the antisymmetric off-diagonal ![]() and given that
and given that
![]() we get altogether
we get altogether
| = | (11) |
| = | 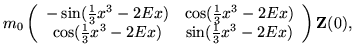 |
(12) |
When the matrices ![]() and
and ![]() are combined to get the complete solution
are combined to get the complete solution
![]() it is helpful to observe that one interpretation of a matrix product is that the second factor forms linear combinations of the columns of the first factor. Doing so, the solutions inherent in the matrix
it is helpful to observe that one interpretation of a matrix product is that the second factor forms linear combinations of the columns of the first factor. Doing so, the solutions inherent in the matrix ![]() are just rewritten in the basis defined by
are just rewritten in the basis defined by ![]() ,
but otherwise interpreted as any other soluton would be.
,
but otherwise interpreted as any other soluton would be.
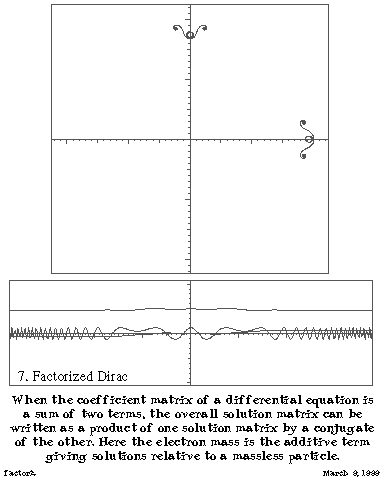 |
Figure 2 shows how little the mass eventually matters in comparison to the energy for a consistently increasing potential such as the parabolic potential well of the harmonic oscillator. On the other hand, near the classical turning points and through the forbidden zone, there are appreciable discrepancies which are more clearly evident in the diagrams of the factored potential than they were in their original form.
In principle, there is no reason why the factorization implementing the law of exponents for matrices should not be performed in the opposite order, regarding the mass term as fndamental. It would simply generate hyperbolic functions, with respect to which the energy terms would drive a rotating mirror which could be expected to raise and lower amplitudes passing from resonances to antiresonances.
After all, the final result is independent of the order of factorization.
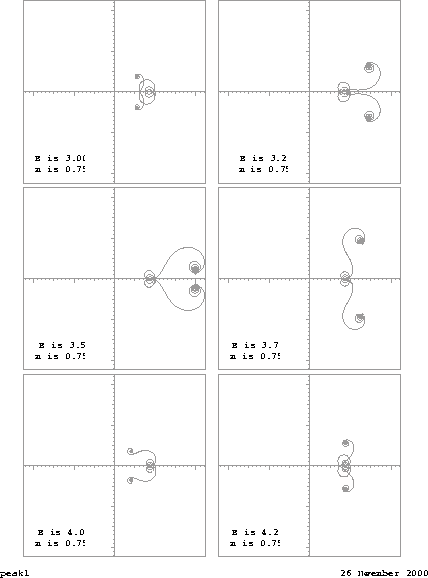 |
In Figure 3 a series of six phase planes is shown, straddling the interval of energies between one resonance and the next. The point to be observed is the changing relationship between the amplitude of the interior wave function and the amplitude of the exterior wave function. The phase planes are shown separately to make the progression of ratios clearly evident. But then, for purposes of comparison, all six planes have been superimposed in Figure 4, where the magnitude of the variation is easier to discern.
 |