

Next: Extremos libres
Up: Cadena homogénea
Previous: Cadena homogénea
Contents
Para este caso todas las matrices de Transferencia son de la
forma
![\begin{displaymath}
T \left[ \begin{array}{ccc}
\frac{\lambda - a_{0}}{a_{1}} & -1 \\
1 & 0
\end{array} \right]
\end{displaymath}](img145.png) |
(III.4) |
donde
Como ya se ha mencionado antes, con una Cadena homogénea,
el producto de matrices de Transferencia resulta ser la matriz
elevada a una potencia igual a la longitud de la misma,
explícitamente la Ec. (II.17) se convierte en
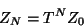 |
(III.6) |
Calculemos los Eigenvalores y Eigenvectores de 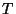 para poder
evaluar cualquier potencia de ella, pero antes denotemos
para poder
evaluar cualquier potencia de ella, pero antes denotemos
 |
(III.7) |
entonces la Ec. característica de 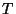 es
es
![\begin{displaymath}
\left[ \begin{array}{ccc}
c - \mu & -1 \\
1 & -\mu
\end{array} \right] = 0
\end{displaymath}](img153.png) |
(III.8) |
explícitamente
a la relación de arriba es lo que se conoce como Relación de
Dispersión; si se hace la sustitución
 |
(III.9) |
se obtiene
pero como
entonces
finalmente
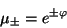 |
(III.10) |
ahora bien, los elementos de la Matriz de Transferencia son
reales, por lo que podemos hacer las siguientes conclusiones, de
las Ecs. (III.7) y (III.9):
- i)
- Si
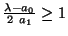 entonces
entonces 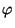 es real, y dependiendo en el signo, corresponde a una
propagación de las ondas en forma exponencial creciente o
decreciente para
es real, y dependiendo en el signo, corresponde a una
propagación de las ondas en forma exponencial creciente o
decreciente para 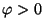 ó
ó 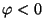 respectivamente.
respectivamente.
- ii)
- Si
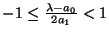 entonces
entonces
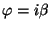 ,
que corresponde a una propagación oscilatoria.
,
que corresponde a una propagación oscilatoria.
- iii)
- Finalmente si
 implica
que
implica
que
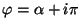 y se trata de un tipo de
oscilación creciente o decreciente, dependiendo en el
signo de
y se trata de un tipo de
oscilación creciente o decreciente, dependiendo en el
signo de 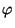 , ya que en este caso las partículas
vecinas alternan en el signo de sus desplazamientos.
, ya que en este caso las partículas
vecinas alternan en el signo de sus desplazamientos.
Es claro de la Ec. (III.10) que en cada caso ocurren los dos
posibles, y así como ejemplo en el segundo, la combinación
da lugar a la propagación de una Onda viajera.
Después del análisis anterior, calculamos los Eigenvectores
correspondientes
de la segunda relación
por lo tanto
explícitamente
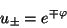 |
(III.11) |
Para los Eigenvectores izquierdos se tiene
utilizando la segunda ecuación
de donde
finalmente
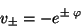 |
(III.12) |
Para hacer uso del Teorema Espectral, calculemos los Operadores
de Proyección correspondientes, haciendo uso de la notación
de Dirac
ahora bien
y
haciendo uso de las Ecs. (III.11) y (III.12), se tiene
o también
![\begin{displaymath}
P _{+} = \frac{ \left[ \begin{array}{ccc}
e^{\varphi} & ...
... -e^{-\varphi}
\end{array} \right]}{2 \mbox{senh} \ \varphi}
\end{displaymath}](img180.png) |
(III.13) |
y
![\begin{displaymath}
P _{-} = \frac{ \left[ \begin{array}{ccc}
-e^{-\varphi} &...
... & e^{\varphi}
\end{array} \right]}{2 \mbox{senh} \ \varphi}
\end{displaymath}](img182.png) |
(III.14) |
con lo anterior podemos escribir
![\begin{displaymath}
T = \frac{e^{\varphi}}{2 \mbox{senh} \varphi} \left[
\begi...
...
-e^{-\varphi} & 1 \\
-1 & e^{\varphi}
\end{array} \right]
\end{displaymath}](img183.png) |
(III.15) |
Aplicando el Teorema de Sylvester
finalmente
![\begin{displaymath}
T^{N} = \frac{1}{\mbox{senh } \varphi} \left[
\begin{array...
... \varphi & - \mbox{senh} ( N - 1)\varphi
\end{array} \right]
\end{displaymath}](img186.png) |
(III.16) |
Entonces de las Ecs. (II.25) y (III.16), se tiene la siguiente
Ec. que nos determina las frecuencias posibles de vibración
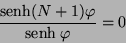 |
(III.17) |
como
se tiene que
la Ec. anterior se cumple para los siguientes valores
de donde
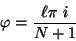 |
(III.18) |
nos interesa el cosh 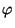 , que podemos calcularlo
de la Ec. de arriba y que es
, que podemos calcularlo
de la Ec. de arriba y que es
pero de las Ecs (III.9) y (III.7) se puede escribir
finalmente se obtienen las frecuencias de resonancia que
están dadas por la siguiente relación
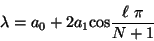 |
(III.19) |
los valores de 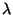 dados por la Ec. de arriba son
los únicos posibles. A primera vista se obtienen más de
dados por la Ec. de arriba son
los únicos posibles. A primera vista se obtienen más de 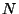 frecuencias distintas; pero en principio el
frecuencias distintas; pero en principio el 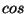 es una función
par, por lo tanto los argumentos negativos proporcionan un valor
idéntico al de los positivos; restan los valores de
es una función
par, por lo tanto los argumentos negativos proporcionan un valor
idéntico al de los positivos; restan los valores de 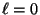 y
y
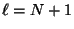 , pero de la Ec (III.18) se tiene que
, pero de la Ec (III.18) se tiene que  y
y
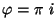 respectivamente, que se tienen que eliminar
porque de lo contrario, desde el punto de vista físico nos
dicen que todas las partículas tienen el mismo
desplazamiento, lo cual es falso porque estamos tratando con una
red lineal con extremos fijos, entonces
respectivamente, que se tienen que eliminar
porque de lo contrario, desde el punto de vista físico nos
dicen que todas las partículas tienen el mismo
desplazamiento, lo cual es falso porque estamos tratando con una
red lineal con extremos fijos, entonces 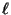 en la Ec. (III.19)
sólo puede tomar los valores
en la Ec. (III.19)
sólo puede tomar los valores 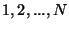 .
Para obtener las componentes de los Modos Normales de
Vibración, hacemos uso de la Ec.
.
Para obtener las componentes de los Modos Normales de
Vibración, hacemos uso de la Ec.
ya que sabemos como obtener 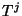 y que es
y que es
de donde
haciendo uso de la Ec. (III.18), se tiene
o también
si hacemos
que siempre es posible, se obtiene finalmente
 |
(III.20) |
que es la componente 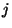 del Eigenvector
del Eigenvector 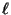



Next: Extremos libres
Up: Cadena homogénea
Previous: Cadena homogénea
Contents
Pedro Hernandez
2006-02-20
![\begin{eqnarray*}
\arrowvert u_\pm >< v_\pm \arrowvert &=& \left [
\begin{arra...
...ccc}
v_\pm & 1 \\
v_\pm \ u_\pm & u_\pm
\end{array} \right]
\end{eqnarray*}](img177.png)
![\begin{eqnarray*}
< v_\pm \arrowvert u_\pm > &=& \left [
\begin{array}{ccc}
v...
... 1 \\
u_\pm
\end{array} \right]
\\
& = & v_\pm + \ u_\pm
\end{eqnarray*}](img178.png)
![\begin{displaymath}
P _{+} = \frac{ \left[ \begin{array}{ccc}
-e^{\varphi} & ...
...{-\varphi}
\end{array} \right]}{-e^{\varphi} + e^{-\varphi}}
\end{displaymath}](img179.png)
![\begin{displaymath}
P _{+} = \frac{ \left[ \begin{array}{ccc}
e^{\varphi} & ...
... -e^{-\varphi}
\end{array} \right]}{2 \mbox{senh} \ \varphi}
\end{displaymath}](img180.png)
![\begin{displaymath}
P _{-} = \frac{ \left[ \begin{array}{ccc}
-e^{-\varphi} &...
...^{\varphi}
\end{array} \right]}{-e^{-\varphi} + e^{\varphi}}
\end{displaymath}](img181.png)
![\begin{displaymath}
P _{-} = \frac{ \left[ \begin{array}{ccc}
-e^{-\varphi} &...
... & e^{\varphi}
\end{array} \right]}{2 \mbox{senh} \ \varphi}
\end{displaymath}](img182.png)
![\begin{displaymath}
= \frac{1}{2 \mbox{senh} \varphi} \left[
\begin{array}{ccc...
...^{(N - 1)\varphi}
-e^{-(N - 1)\varphi})
\end{array} \right]
\end{displaymath}](img185.png)
![\begin{displaymath}
T^{N} = \frac{1}{\mbox{senh } \varphi} \left[
\begin{array...
... \varphi & - \mbox{senh} ( N - 1)\varphi
\end{array} \right]
\end{displaymath}](img186.png)