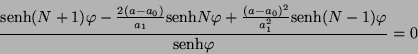Next: Un extremo libre y
Up: Cadena homogénea
Previous: Extremos confinados
Contents
En este caso las únicas Matrices de Transferencia distintas,
son las correspondientes a las partículas 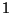 y
y 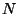 , pero
tienen una forma sencilla, que es la siguiente
, pero
tienen una forma sencilla, que es la siguiente
![\begin{displaymath}
T_{1} = T_{N} = \left[ \begin{array}{ccc}
\frac{\lambda - a}{a_1} & -1 \\
1 & 0
\end{array} \right]
\end{displaymath}](img209.png) |
(III.21) |
donde
y  es la misma de antes.
Esta vez la Ec. (II.17) es
es la misma de antes.
Esta vez la Ec. (II.17) es
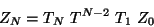 |
(III.22) |
pero es posible transformarla en
como antes
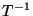 es la matríz inversa de
es la matríz inversa de 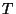 , que
tiene la forma siguiente
, que
tiene la forma siguiente
y 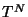 es la misma de la Ec. (III.16).
Calculemos los productos que nos interesan y que en principio
son
es la misma de la Ec. (III.16).
Calculemos los productos que nos interesan y que en principio
son 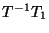 y
y 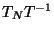
y
efectuemos ahora el producto
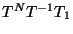
finalmente la matriz anterior por
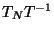
en este caso la Ec. que nos determina las frecuencias es
nuevamente como senh
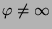 , se tiene
entonces que
, se tiene
entonces que
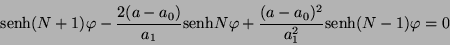 |
(III.23) |
las soluciones de la Ec. de arriba no son muy obvias,
hay necesidad de utilizar métodos numéricos para obtenerlas,
en este trabajo no resolvemos directamente las Ecs. sino que
diagonalizamos la Matriz de Movimiento para obtener el cuadrado de
las frecuencias naturales del sistema, más adelante se
mostrarán los resultados, que se obtienen para modelos de
cadenas unidimensionales más complicados que el anterior.




Next: Un extremo libre y
Up: Cadena homogénea
Previous: Extremos confinados
Contents
Pedro Hernandez
2006-02-20
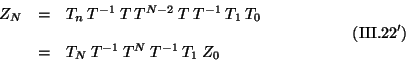
![\begin{displaymath}
T = \left [ \begin{array}{cc}
\frac{\lambda - a_{0}}{a_{1}} & -1 \\
\\
1 & 0
\end{array} \right]
\end{displaymath}](img214.png)
![\begin{displaymath}
\left [ \begin{array}{cc}
0 & 1 \\
\\
-1 & \frac{\lambda - a_{0}}{a_{1}}
\end{array} \right]
\end{displaymath}](img216.png)
![\begin{eqnarray*}
T^{-1} T_{1} & = & \left [ \begin{array}{cc}
0 & 1 \\
\\ ...
...& 0 \\
\\
\frac{a - a_{0}}{a_{1}} & 1
\end{array} \right]
\end{eqnarray*}](img220.png)
![\begin{eqnarray*}
T_{N} T^{-1} & = & \left [ \begin{array}{cc}
\frac{\lambda -...
... -\frac{a - a_{0}}{a_{1}} \\
\\
0 & 1
\end{array} \right]
\end{eqnarray*}](img221.png)
![\begin{eqnarray*}
T^{N} T^{-1} T_{1} & = & \frac{1}{\mbox{senh} \varphi} \left ...
... -
1)\varphi & -\mbox{senh}(N - 1)\varphi
\end{array} \right]
\end{eqnarray*}](img223.png)
![\begin{eqnarray*}
\tau & = & \left [\begin{array}{cc}
1 & - \frac{a - a_{0}}{a...
...
1) \varphi & -\mbox{senh} (N - 1)\varphi
\end{array} \right]
\end{eqnarray*}](img224.png)