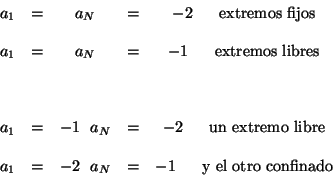Next: Extremos confinados
Up: Análisis de diferentes modelos
Previous: Análisis de diferentes modelos
Contents
En este modelo se considera, que todas las masas de las
partículas son iguales, lo mismo que las constantes de
resorte, por lo que es posible obtener una solución
analítica para el comportamiento de dicha cadena, es decir,
podemos obtener explícitamente y de una forma sencilla, las
frecuencias de resonancia y los modos normales de vibración.
Entonces lo que se considera es
y la matriz de movimiento tiene la forma muy sencilla
![\begin{displaymath}
A = \frac{k}{m} \left[ \begin{array}{cccccc}
a_{1} & 1 & &...
...ddots & \ddots & 1 \\
& & & 1 & a_{N}
\end{array} \right]
\end{displaymath}](img141.png) |
(III.2) |
donde  y
y 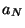 tienen un valor, de acuerdo con
el tipo de condiciones a la frontera que estemos considerando, es
decir
tienen un valor, de acuerdo con
el tipo de condiciones a la frontera que estemos considerando, es
decir
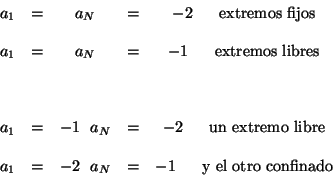 |
(III.3) |
Subsections




Next: Extremos confinados
Up: Análisis de diferentes modelos
Previous: Análisis de diferentes modelos
Contents
Pedro Hernandez
2006-02-20
![\begin{displaymath}
A = \frac{k}{m} \left[ \begin{array}{cccccc}
a_{1} & 1 & &...
...ddots & \ddots & 1 \\
& & & 1 & a_{N}
\end{array} \right]
\end{displaymath}](img141.png)