



Next: Cadena con un defecto
Up: Cadena homogénea
Previous: Extremos libres
Contents
i) Partícula 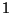 libre.- Para este caso la
única Matriz de Transferencia distinta, es la perteneciente a
dicha partícula y tiene la forma de (III.21), así la
matriz
libre.- Para este caso la
única Matriz de Transferencia distinta, es la perteneciente a
dicha partícula y tiene la forma de (III.21), así la
matriz 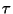 tiene la expresión
tiene la expresión
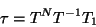 |
(III.24) |
en el caso anterior la hemos obtenido
explícitamente y es
por lo que ahora la Ec. para obtener los Eigenvalores es
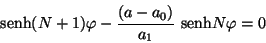 |
(III.25) |
lo mismo que dijimos para las soluciones de (III.23), se
aplica para (III.24) y claramente para el siguiente caso, en el
que la partícula 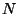 será la libre.
será la libre.
ii) Partícula 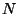 libre.- Ahora
libre.- Ahora 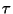 tiene
la estructura
tiene
la estructura
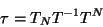 |
(III.26) |
ya conocemos la expresión del producto 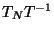 sólo resta
multiplicarlo por
sólo resta
multiplicarlo por 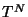 , con lo que se obtiene lo siguiente
, con lo que se obtiene lo siguiente
la Ec. deseada es
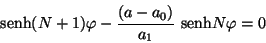 |
(III.27) |
que es idéntica a (III.25), que es un resultado que ya
se esperaba.




Next: Cadena con un defecto
Up: Cadena homogénea
Previous: Extremos libres
Contents
Pedro Hernandez
2006-02-20
![\begin{displaymath}
\tau = \frac{1}{\mbox{senh} \varphi} \left[ \begin{array}{c...
...hi & \qquad -\mbox{senh} (N - 1) \varphi
\end{array} \right]
\end{displaymath}](img229.png)
![]() libre.- Ahora
libre.- Ahora ![]() tiene
la estructura
tiene
la estructura
![\begin{eqnarray*}
\tau & = & \left[ \begin{array}{ccc}
1 & \frac{-(a - a_{0})}...
...\ N \varphi & -\mbox{senh} (N - 1) \varphi
\end{array} \right]
\end{eqnarray*}](img232.png)