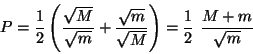


Next: Cadena con variación lineal
Up: Análisis de diferentes modelos
Previous: Defecto en la constante
Contents
Ahora finalizaremos el modelo más simple de un cristal en
cuya estructura intervienen 2 clases de átomos, esta vez nuestro
modelo consiste de una red unidimensional en la cual, el valor de
la masa de cada una de las partículas alterna, en la figura
siguiente se muestra el modelo de cadena que consideraremos
Como siempre, si consideraremos una red diatómica con
extremos fijos, la Matriz de Movimiento en su forma simétrica es
![\begin{displaymath}
\left[ \begin{array}{cccc}
\frac{-2k}{M} & \frac{k}{\sqrt{...
...{Mm}} \\
& & \\
0 & \ddots & \ddots
\end{array} \right]
\end{displaymath}](img296.png) |
(III.37) |
se observa que todos los elementos de las diagonales
superior e inferior de la principal son iguales y en la diagonal
principal alternan los valores.
Para las relaciones de recurrencia tenemos que hacer la
distinción entre partículas pares e impares, así se
tiene
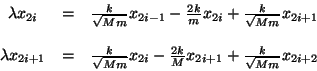 |
(III.38) |
entonces las Matrices de Tranferencia tiene la siguiente
estructura
es claro que también las Matrices de Transferencia
alternan, por lo tanto es conveniente considerar a las
partículas por parejas, en otras palabras, considerar la
celda unitaria constituida de dos átomos, entonces la Matriz de
Transferencia adecuada es el producto de las dos de arriba, si
antes de efectuar el producto utilizamos las siguientes notaciones
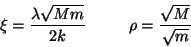 |
(III.39) |
donde 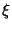 la podemos interpretar como una frecuencia
normalizada por la razón del promedio geométrico de las masas
y el promedio aritmético de dos resortes, y a
la podemos interpretar como una frecuencia
normalizada por la razón del promedio geométrico de las masas
y el promedio aritmético de dos resortes, y a 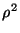 como la
razón de masas.
Además
como la
razón de masas.
Además
 |
(III.40) |
que en términos de 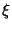 y
y 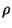 quedan
quedan
calculemos el producto deseado
finalmente
![\begin{displaymath}
T_{D} = \left[ \begin{array}{cc}
\alpha \beta - 1 & -\alpha \\
& \\
\beta & -1
\end{array} \right]
\end{displaymath}](img307.png) |
(III.41) |
La Ec. característica de 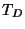 es
es
explícitamente
finalmente la relación de dispersión en términos
de 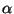 y
y 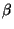 es
es
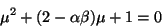 |
(III.42) |
haciendo uso de las expresiones para 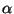 y
y 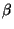 en función de los parámetros
en función de los parámetros 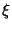 y
y 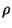 , podemos expresar
a (III.42) en términos de éstos, pero antes calculemos el
producto de
, podemos expresar
a (III.42) en términos de éstos, pero antes calculemos el
producto de 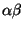
![\begin{displaymath}
\alpha \beta = 2(\xi + \rho) \cdot 2(\xi + \frac{1}{\rho}) =
4\left[\xi^{2} + \xi(\rho + \frac{1}{\rho}) + 1\right]
\end{displaymath}](img316.png) |
(III.43) |
si se introduce otro nuevo parámetro
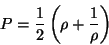 |
(III.44) |
haciendo uso de la expresión para 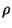 ,
, 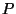 en
términos de las masas tiene la forma
en
términos de las masas tiene la forma
así 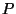 resulta ser la razón del promedio
aritmético al promedio geométrico de las masas, si ahora
sustituimos
resulta ser la razón del promedio
aritmético al promedio geométrico de las masas, si ahora
sustituimos 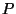 en
en 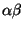 , y la última en la
relación de dispersión, ésta toma la forma
, y la última en la
relación de dispersión, ésta toma la forma
finalmente
por simplicidad en el álgebra obtenemos los números
de onda de (III.42)
o también
es claro que
veamos cual es la frontera entre los  reales y
complejos, que está dada por la Ec.
reales y
complejos, que está dada por la Ec.
si hacemos uso de (III.43), la Ec. de arriba en
función de 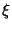 y
y 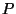 es
es
también es posible expresar como
con lo que tenemos dos alternativas
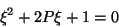 |
(III.45) |
ó
la segunda de las Ecs. de arriba, nuevamente nos proporciona
dos alternativas
ó
la Ec. (III.45) es una hipérbola cuyas asíntotas
son las Ecs. (III.46).
Ahora analicemos la relación de dispersión en términos de
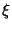 y
y 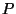 , utilizando la Ec. (III.42') se tiene
, utilizando la Ec. (III.42') se tiene
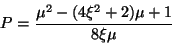 |
(III.47) |
considerando a  como una constante, se tiene que
como una constante, se tiene que
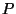 es una fracción racional en
es una fracción racional en 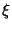 cuya gráfica es una
hipérbola, ya que se sabe que una fracción racional de segundo
grado representa una hipérbola.
La Ec. (III.47) tiene un sólo polo en
cuya gráfica es una
hipérbola, ya que se sabe que una fracción racional de segundo
grado representa una hipérbola.
La Ec. (III.47) tiene un sólo polo en 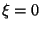 y sus raíces
están dadas por
y sus raíces
están dadas por
entonces éstas son
es claro que existirán unicamente para valores de
 positivos, en otras palabras si se hace una gráfica de
positivos, en otras palabras si se hace una gráfica de 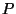 versus
versus 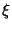 , considerando a
, considerando a  como constante, existirán 2
clases de hipérbolas, unas que cortan al eje
como constante, existirán 2
clases de hipérbolas, unas que cortan al eje 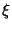 y otras que
no lo hacen. La siguiente figura nos muestra los aspectos
mencionados anteriormente
Se observa en la figura las tres distintas regiones que
corresponden a los diferentes valores de
y otras que
no lo hacen. La siguiente figura nos muestra los aspectos
mencionados anteriormente
Se observa en la figura las tres distintas regiones que
corresponden a los diferentes valores de  con énfasis en
la frontera que separa a las regiones donde
con énfasis en
la frontera que separa a las regiones donde  es real y donde
ésta es compleja. Extrictamente hablando la única porción
del plano
es real y donde
ésta es compleja. Extrictamente hablando la única porción
del plano 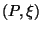 que nos interesa, ya que es la
físicamente aceptable, es aquella que parte de la recta
tangente a la hipérbola frontera, cuya ecuación es
que nos interesa, ya que es la
físicamente aceptable, es aquella que parte de la recta
tangente a la hipérbola frontera, cuya ecuación es
y eso se debe a que 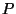 únicamente puede asumir los
valores mayores que
únicamente puede asumir los
valores mayores que 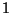 y a lo más puede ser igual a
y a lo más puede ser igual a 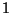 , vemos
que cuando lo último ocurre, existe un intervalo continuo para
, vemos
que cuando lo último ocurre, existe un intervalo continuo para
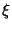 , pero en el momento en que
, pero en el momento en que 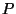 comienza a crecer, es decir,
las masas empiezan a diferir, existen tres regiones muy bien
marcadas; la primera en que los valores de
comienza a crecer, es decir,
las masas empiezan a diferir, existen tres regiones muy bien
marcadas; la primera en que los valores de 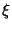 son muy
pequeños y que se encuentra entre el eje
son muy
pequeños y que se encuentra entre el eje 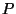 y la hipérbola
frontera representada por la Ec.(III.45); la segunda que es una
región prohibida porque en este caso
y la hipérbola
frontera representada por la Ec.(III.45); la segunda que es una
región prohibida porque en este caso 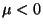 , que implica un
fuerte amortiguamiento de la propagación, ésta se encuentra
dentro de la rama de la hipérbola frontera. Finalmente, se tiene
una tercera, localizada entre la frontera y la recta
, que implica un
fuerte amortiguamiento de la propagación, ésta se encuentra
dentro de la rama de la hipérbola frontera. Finalmente, se tiene
una tercera, localizada entre la frontera y la recta  ,
donde en valor absoluto estas frecuencias crecen rápidamente.
Pudiera ocurrir que ciertas frecuencias cayeran en la región
donde
,
donde en valor absoluto estas frecuencias crecen rápidamente.
Pudiera ocurrir que ciertas frecuencias cayeran en la región
donde  , que implicaría una propagación exponencial
creciente, pero de la relación de dispersión sabemos que su
recíproco también es un eigenvalor de la Matriz de
Transferencia, y esta
, que implicaría una propagación exponencial
creciente, pero de la relación de dispersión sabemos que su
recíproco también es un eigenvalor de la Matriz de
Transferencia, y esta  cancelaría el crecimiento
exponencial de la propagación.
cancelaría el crecimiento
exponencial de la propagación.
Figura 3.8:
Gráfica del negativo del cuadrado de las frecuencias
naturales de una cadena diatómica de 8 partículas, donde
se varia la razón de masas en el eje vertical.
|
|
Mediante el programa TRIDI se ha obtenido el espectro de
frecuencias para una red diatómica, en la que se varía la
razón de masas en una manera exponencial, la gráfica de este
espectro corres-ponde a la Fig. (3.8), donde se observa el
comportamiento descrito antes, es decir, tres regiones, una de
frecuencias bajas, otra donde no se encuentra ninguna frecuencia y
una tercera de frecuencias altas.
También se han obtenido los Modos Normales y se han
graficado como lo muestra la Fig. (3.9).
La cadena es de 8 partículas, esta vez el parámetro que
se varía es la razón de masas 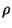 desde un valor igual a
desde un valor igual a
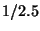 hasta
hasta 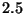 ; la parte inferior de cada Modo corresponde al
de una cadena con su primera partícula ligera, después van
alternando en pesada, ligera, etc., y en la parte superior se
convierte en partícula pesada, ligera pesada, etc.
Se observa que se tienen en realidad dos cadenas, una formada
por partículas ligeras y otra de pesadas; en los Modos de la
izquierda que corresponden a los Opticos en orden descendente,
éstas se comportan en forma antagónica en sus desplazamientos,
mientras que en los Acústicos, que son los de la derecha en el
mismo orden anterior, éstas se comportan con cooperación en
sus desplazamientos.
En los Modos Opticos las partículas ligeras son las que
siempre tienen mayor amplitud, con excepción del tercer Modo ya
que las partículas
; la parte inferior de cada Modo corresponde al
de una cadena con su primera partícula ligera, después van
alternando en pesada, ligera, etc., y en la parte superior se
convierte en partícula pesada, ligera pesada, etc.
Se observa que se tienen en realidad dos cadenas, una formada
por partículas ligeras y otra de pesadas; en los Modos de la
izquierda que corresponden a los Opticos en orden descendente,
éstas se comportan en forma antagónica en sus desplazamientos,
mientras que en los Acústicos, que son los de la derecha en el
mismo orden anterior, éstas se comportan con cooperación en
sus desplazamientos.
En los Modos Opticos las partículas ligeras son las que
siempre tienen mayor amplitud, con excepción del tercer Modo ya
que las partículas  y
y 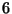 forman un Nodo de la Cadena,
mientras que en los Acústicos es claro que quienes tienen los
desplazamientos son las partículas pesadas y las ligeras
vibran como ellas lo hacen, nuevamente con excepción del sexto
Modo en las que las partículas
forman un Nodo de la Cadena,
mientras que en los Acústicos es claro que quienes tienen los
desplazamientos son las partículas pesadas y las ligeras
vibran como ellas lo hacen, nuevamente con excepción del sexto
Modo en las que las partículas  y
y  vuelven a formar un
Nodo.
Asimismo se ve que la última partícula en la parte
superior de cada Modo, tiene un desplazamiento positivo si éste
es par y negativo si es impar.
Finalmente, como siempre en el Modo de más baja frecuencia la
cadena se desplaza como un todo. En el apéndice E se muestra el
listado del programa TRIDI.
Se tiene otro programa llamado TRIVD que varía la masa de
una de las partículas pertenecientes a una cadena diatómica
con una razón de masas fija.
Cuando hicimos el análisis de una red homogénea con un
defecto en masa, mencionamos que el comportamiento de una cadena
arbitraria con defecto es similar al de una homogénea análoga,
así que esta vez que se tiene una diatómica con defecto,
uno debe esperar un comportamiento similar al de la homogénea.
Se han obtenido resultados tanto para una cadena con un
número par de partículas como para una con un número
impar.
En la Fig. (3.10) se muestra el Espectro para una red de 8
partículas que tiene el defecto en la partícula 4, la
única diferencia que se observa con el de la Fig. (3.2), es que
existe una banda prohibida en la que no se localiza ninguna
frecuencia.
vuelven a formar un
Nodo.
Asimismo se ve que la última partícula en la parte
superior de cada Modo, tiene un desplazamiento positivo si éste
es par y negativo si es impar.
Finalmente, como siempre en el Modo de más baja frecuencia la
cadena se desplaza como un todo. En el apéndice E se muestra el
listado del programa TRIDI.
Se tiene otro programa llamado TRIVD que varía la masa de
una de las partículas pertenecientes a una cadena diatómica
con una razón de masas fija.
Cuando hicimos el análisis de una red homogénea con un
defecto en masa, mencionamos que el comportamiento de una cadena
arbitraria con defecto es similar al de una homogénea análoga,
así que esta vez que se tiene una diatómica con defecto,
uno debe esperar un comportamiento similar al de la homogénea.
Se han obtenido resultados tanto para una cadena con un
número par de partículas como para una con un número
impar.
En la Fig. (3.10) se muestra el Espectro para una red de 8
partículas que tiene el defecto en la partícula 4, la
única diferencia que se observa con el de la Fig. (3.2), es que
existe una banda prohibida en la que no se localiza ninguna
frecuencia.
Figura 3.10:
Gráfica del negativo del cuadrado de las
frecuencias naturales de una cadena diatómica de 8 partículas,
variando en el eje vertical la masa de la partícula 4.
|
|
Se muestran los Modos correspondientes en la Fig. (3.11), donde
es clara la similaridad entre el comportamiento de estos Modos y
los de la Fig. (3.3), por lo que no repetiremos lo expuesto para
aquélla.
La Fig (3.12) muestra el Espectro para una cadena de 7
partículas, cuya partícula 3 constituye el defecto, se
observa que esta vez existe una frecuencia, la número 4 en orden
descendente, que penetra en la región prohibida, cosa que no
ocurre para un número par de partículas, por lo demás el
comportamiento del Espectro es similar al de la cadena homogénea
con defecto.
Por simetría sólo se grafican 6 de los 7 Modos de esta
cadena, la Fig. (3.13) nos lo muestra, pero es clara la tendencia
de que el último Modo tenga comportamiento similar al Modo de
más baja frecuencia de la cadena de 8 partículas. Asimismo
se observa que el comportamiento de todos los Modos es similar a
los de una homógenea con defecto, por lo que tampoco repetiremos
lo expuesto para aquél modelo. En el Apéndice F se encuentra
el listado del programa TRIVD.
En los modelos que siguen, no se obtuvieron expresiones
explícitas para obtener las frecuencias como se ha venido
haciendo hasta ahora, porque éstos no tienen expresiones simples
para su Ec. característica que puedan interpretarse, es por
ello, que únicamente se muestran los resultados obtenidos por
computadora.
Figura 3.12:
Gráfica del negativo del cuadrado de las frecuencias
naturales de una cadena diatómica de 8 particulas variando en el
eje vertical la masa de la partícula 3.
|
|



Next: Cadena con variación lineal
Up: Análisis de diferentes modelos
Previous: Defecto en la constante
Contents
Pedro Hernandez
2006-02-20
![\includegraphics[width=4.7in]{f10p62.eps}](img295.png)
![\includegraphics[width=4.7in]{f10p62.eps}](img295.png)
![\begin{displaymath}
\left[ \begin{array}{cccc}
\frac{-2k}{M} & \frac{k}{\sqrt{...
...{Mm}} \\
& & \\
0 & \ddots & \ddots
\end{array} \right]
\end{displaymath}](img296.png)
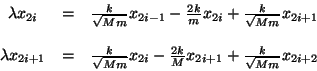
![\begin{displaymath}
\left[ \begin{array}{cccc}
(\lambda + \frac{2k}{m}) \frac{...
... 0
\end{array} \right] \qquad \mbox{part\'{\i}culas \ pares}
\end{displaymath}](img298.png)
![\begin{displaymath}
\; \; \; \left[ \begin{array}{cccc}
(\lambda + \frac{2k}{m...
...
\end{array} \right] \qquad \mbox{part\'{\i}culas \ impares}
\end{displaymath}](img299.png)
![\begin{displaymath}
T_{D} = \left[ \begin{array}{cc}
\alpha & -1 \\
& \\
...
...ray}{cc}
\beta & -1 \\
& \\
1 & 0
\end{array} \right]
\end{displaymath}](img306.png)
![\begin{displaymath}
T_{D} = \left[ \begin{array}{cc}
\alpha \beta - 1 & -\alpha \\
& \\
\beta & -1
\end{array} \right]
\end{displaymath}](img307.png)
![\begin{displaymath}
\left[ \begin{array}{cc}
\alpha \beta - 1 -\mu & -\alpha \\
& \\
\beta & -1 -\mu
\end{array} \right] = 0
\end{displaymath}](img309.png)