



Next: Parametrización de rotaciones hiperbólicas
Up: Diversos aspectos de la
Previous: Expresiones para el producto
Contents
El análisis de la representación geométrica de las
Matrices Unimodulares de dimensión dos es como sigue; ya hemos
visto que es posible repesentar toda matriz unimodular como la
exponencial del producto entre un ángulo y un ``vector'' éste
último está definido en un espacio cuyos ``vectores'' base son
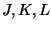 ; además este espacio tiene una norma definida por
(IV.8).
Se tenía la definición para una cierta
; además este espacio tiene una norma definida por
(IV.8).
Se tenía la definición para una cierta 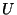 en la forma
en la forma
donde 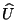 es un ``vector unitario'', por lo
que podemos decir que la magnitud de
es un ``vector unitario'', por lo
que podemos decir que la magnitud de 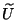 es
es
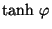 , y a
, y a 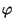 como veremos más adelante
tendremos que interpretarlo como un cierto ángulo de rotación;
además de (IV.18b)
como veremos más adelante
tendremos que interpretarlo como un cierto ángulo de rotación;
además de (IV.18b) 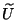 también tiene la
expresión
también tiene la
expresión
ya que los elementos de nuestra matriz son reales,
entonces los elementos de 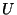 también son reales, lo mismo que
el
también son reales, lo mismo que
el
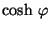 , por lo tanto tenemos un conjunto de
``vectores'' reales, que nos son otra cosa que un conjunto de
repesentaciones para las Matrices Unimodulares.
Consideremos el ``vector'' unitario
, por lo tanto tenemos un conjunto de
``vectores'' reales, que nos son otra cosa que un conjunto de
repesentaciones para las Matrices Unimodulares.
Consideremos el ``vector'' unitario
cuya norma expresada en función de sus componentes es
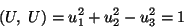 |
(IV.21) |
que se reconoce com la Ec. de un hiperboloide de una
sóla rama, debido a lo anterior podemos decir que todos los
``vectores'' unitarios definen una superficie hiperbólica de una
sóla rama.




Next: Parametrización de rotaciones hiperbólicas
Up: Diversos aspectos de la
Previous: Expresiones para el producto
Contents
Pedro Hernandez
2006-02-20