


Next: Condición para obtener los
Up: Diversos aspectos de la
Previous: Representación geométrica
Contents
Cuando uno trabaja en el espacio ordinario, es decir, donde los
vectores unitarios definen una superficie esférica en tres
dimensiones, una parametrización conveniente para las Rotaciones
es la que hace uso de Involuciones [20], que consiste en
descomponer la rotación como el producto de dos Involuciones,
matricialmente
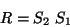 |
(IV.22) |
donde
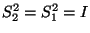 el procedimiento consiste en seleccionar dos ejes en el
plano ecuatorial, éste es aquel plano perpendicular al eje de
rotación, de tal forma que el ángulo que los separe sea la
mitad del ángulo de rotación, ya que se sabe que la rotación
está representada por el arco que une a dichos ejes y cuya
longitud es la mitad del ángulo.
Si después uno desea efectuar otra rotación, se
seleccionan los dos ejes correspondientes de manera adecuada,
sólo que el primero se hace coincidir con el de la Segunda
Involución de la primera rotación, de tal forma que la
rotación que resulta está representada como la suma de los dos
arcos, en forma matricial
el procedimiento consiste en seleccionar dos ejes en el
plano ecuatorial, éste es aquel plano perpendicular al eje de
rotación, de tal forma que el ángulo que los separe sea la
mitad del ángulo de rotación, ya que se sabe que la rotación
está representada por el arco que une a dichos ejes y cuya
longitud es la mitad del ángulo.
Si después uno desea efectuar otra rotación, se
seleccionan los dos ejes correspondientes de manera adecuada,
sólo que el primero se hace coincidir con el de la Segunda
Involución de la primera rotación, de tal forma que la
rotación que resulta está representada como la suma de los dos
arcos, en forma matricial
pero
por lo tanto
La Fig. (4.1) nos muestra gráficamente lo anterior.
Entonces se tiene una suma ``vectorial'', donde cada ``vector''
representa un arco de ecuador, cuya longitud es la mitad del
ángulo de la rotación que está representado. Análogamente
en este espacio hiperbólico también es posible la
parametrización, sólo que ahora los arcos no corresponden a
los de círculos máximos, sino que pueden ser de dos clases,
dependiendo en la orientación del ``vector'' de rotación, o de
una elipse o de una hipérbola.
La demostración de dicha Parametrización es como sigue:
Consideremos dos ``vectores''
cuya norma en esta métrica es unitaria, en otras
palabras pertenecen al Hiperboloide unitario, explícitamente
calculemos los productos
 y
y
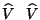 que tienen las expresiones
que tienen las expresiones
ya conocemos el valor del producto interior, sólo
resta efectuar el producto vectorial, de la Ec. (IV.14) se tiene
análogamente
que era de esperarse ya que el producto es antisimétrico; por
lo tanto
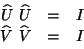 |
(IV.23) |
las Ecs. de arriba nos dicen que 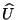 y
y
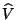 representan una Involución cada una de ellas.
Ahora calculemos el siguiente producto interior.
representan una Involución cada una de ellas.
Ahora calculemos el siguiente producto interior.
donde hemos hecho uso de (IV.14), ahora de (IV.21) se tiene
Si definimos
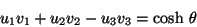 |
(IV.24) |
podemos interpretar la Ec.s de arriba como la
proyección de un vector en el otro, extríctamente
deberíamos multiplicar el
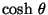 por el
producto de las magnitudes de
por el
producto de las magnitudes de 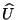 y
y 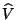 pero
como éstos son unitarios, no hay en este caso necesidad de ello.
Se tiene entonces
pero
como éstos son unitarios, no hay en este caso necesidad de ello.
Se tiene entonces
por lo tanto
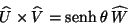 |
(IV.25) |
donde 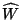 es un``vector'' unitario y
perpendicular en la norma de Lorentz a los ``vectores''
es un``vector'' unitario y
perpendicular en la norma de Lorentz a los ``vectores''
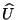 y
y 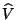 , y cuya magnitud es
, y cuya magnitud es
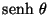 donde
donde 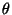 es el angulo que separa a
es el angulo que separa a 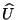 y a
y a
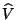 .
De (IV.15) se tiene
.
De (IV.15) se tiene
sustituyendo (IV.24) y (IV.25) en la Ec. de arriba se
llega a la expresión .
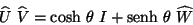 |
(IV.26) |
observemos que el miembro derecho de ésta última es
idéntico al de (IV.10'), y de (IV.10) es posible escribirla como
que nos representa una clase de Rotación que
denominaremos Hiperbólica, lo anterior debido a la métrica que
se tiene. Podemos concluir que siempre es posible factorizar
cualquier rotación hiperbólica
 en el
producto de dos Involuciones, representadas por dos ``vectores''
unitarios
en el
producto de dos Involuciones, representadas por dos ``vectores''
unitarios 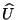 y
y 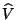 .
El proceso para hallar la representación geométrica de esta
clase de rotaciones consiste en principio, en localizar la
región perpendicular al Polo o Eje de la rotación, que en este
caso es
.
El proceso para hallar la representación geométrica de esta
clase de rotaciones consiste en principio, en localizar la
región perpendicular al Polo o Eje de la rotación, que en este
caso es 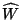 lo cual puede hacerse de la siguiente forma:
Consideremos la expresión del producto interior de los
``vectores''
lo cual puede hacerse de la siguiente forma:
Consideremos la expresión del producto interior de los
``vectores'' 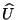 y
y 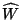
que también es posible escribir como
![\begin{displaymath}
(\widehat{U}, \widehat{W}) = [\widehat{U}, N \widehat{W}] =...
...egin{array}{c}
w_1 \\
w_2 \\
w_3
\end{array} \right]
\end{displaymath}](img474.png) |
(IV.27) |
donde
![\begin{displaymath}
N = \left[ \begin{array}{cccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array} \right]
\end{displaymath}](img475.png) |
(IV.28) |
corresponde a la matriz de métrica en este espacio, es
claro que representa una reflexión en el plano generado por las
coordenadas 1 y 2.
El Ecuador cumple con la siguiente Ec.
explícitamente
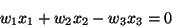 |
(IV.29) |
que se reconoce como la Ec. de un plano que pasa por el
origen, la intersección de éste con el hiperboloide
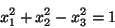 |
(IV.30) |
ya que estamos trabajando en el hiperboloide unitario,
como se sabe en general es una curva plana de segundo grado, cuyas
Ecs. paramétricas son (IV.29) y (IV.30), pero es posible hallar
otra expresión para ellas de la siguiente forma, despejemos de
(IV.29)  con lo que se tiene
con lo que se tiene
elevando al cuadrado
sustituyendo en (IV.30)
finalmente
 |
(IV.31) |
análogamente despejando 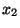 , por el mismo proceso
se obtiene la segunda Ec. paramétrica
, por el mismo proceso
se obtiene la segunda Ec. paramétrica
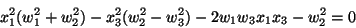 |
(IV.32) |
la primera corresponde a la de un cilindro elíptico
y la segunda a un hiperbolíco. Dependiendo en las coordenadas
de 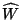 las curvas serán elipses o hipérbolas
únicamente, ya que los casos extremos que serían un
círculo o las asíntotas del hiperboloide no ocurren,
porque eso implicaría que el eje
las curvas serán elipses o hipérbolas
únicamente, ya que los casos extremos que serían un
círculo o las asíntotas del hiperboloide no ocurren,
porque eso implicaría que el eje 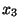 se encuentra sobre
la superficie del hiperboloide, lo cual no es cierto, ni tampoco
lo es que las asíntotas pertenezcan a él.
Ahora ya que tenemos el Ecuador, dado por la Ec. (IV.29), lo
siguiente es seleccionar en ésta a dos ``vectores'' unitarios,
digamos
se encuentra sobre
la superficie del hiperboloide, lo cual no es cierto, ni tampoco
lo es que las asíntotas pertenezcan a él.
Ahora ya que tenemos el Ecuador, dado por la Ec. (IV.29), lo
siguiente es seleccionar en ésta a dos ``vectores'' unitarios,
digamos 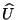 y
y 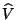 que cumplan con la siguiente
condición y que serán los ejes de las Involuciones
que cumplan con la siguiente
condición y que serán los ejes de las Involuciones
![\begin{displaymath}[\widehat{U}, N \ \widehat{V}]= \mbox{cosh} \ \theta
\end{displaymath}](img487.png) |
(IV.33) |
donde 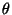 es el ángulo que los separa, éstos
estarán unidos por un arco hiperbólico cuya longitud es
es el ángulo que los separa, éstos
estarán unidos por un arco hiperbólico cuya longitud es
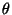 que es un resultado análogo al arco esférico en el
espacio ordinario. Este arco hiperbólico es el que representa
geométricamente a la rotación hiperbólica cuyo ángulo es
que es un resultado análogo al arco esférico en el
espacio ordinario. Este arco hiperbólico es el que representa
geométricamente a la rotación hiperbólica cuyo ángulo es
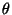 y su eje de rotación es
y su eje de rotación es 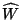 .
Es claro que cualquier pareja de ``vectores'' con separación
angular bien definida representan a una misma rotación
hiperbólica, para eliminar esta ambigüedad se elige a
.
Es claro que cualquier pareja de ``vectores'' con separación
angular bien definida representan a una misma rotación
hiperbólica, para eliminar esta ambigüedad se elige a
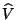 de tal manera que su proyección sobre el plano
de tal manera que su proyección sobre el plano
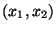 quede a lo largo del eje
quede a lo largo del eje  La Fig. (4.2) nos muestra todo lo anterior para el caso en que
el Ecuador es una elipse.
Finalmente si se desea multiplicar dos matrices Unimodulares,
que en esta representación consiste en combinar dos rotaciones
hiperbólicas y desde el punto de vista geométrico consiste en
lo siguiente:
Hallaremos los correspondientes Ecuadores, después se busca
la intersección de éstos de tal forma que por este punto va a
pasar el eje de la Involución común en ambas rotaciones,
después se forma el arco en un Ecuador cuyo extremo final
coincida con la intersección y de ahí se mide el otro arco
que corresponde a la segunda rotación, en el Ecuador
correspondiente; para acabar se unen los puntos inicial y final
mediante el arco de una curva, que se encuentra en un plano que
pasa por estos puntos, con lo anterior se tiene el arco, que es la
suma ``vectorial'' de dos originales y que representa a la
rotación resultante. En general no conmutará la suma anterior
que es un resultado esperado ya que las matrices no conmutan bajo
la multiplicación.
La Fig (4.3) nos muestra una suma ``vectorial'' de esta clase
La Fig. (4.2) nos muestra todo lo anterior para el caso en que
el Ecuador es una elipse.
Finalmente si se desea multiplicar dos matrices Unimodulares,
que en esta representación consiste en combinar dos rotaciones
hiperbólicas y desde el punto de vista geométrico consiste en
lo siguiente:
Hallaremos los correspondientes Ecuadores, después se busca
la intersección de éstos de tal forma que por este punto va a
pasar el eje de la Involución común en ambas rotaciones,
después se forma el arco en un Ecuador cuyo extremo final
coincida con la intersección y de ahí se mide el otro arco
que corresponde a la segunda rotación, en el Ecuador
correspondiente; para acabar se unen los puntos inicial y final
mediante el arco de una curva, que se encuentra en un plano que
pasa por estos puntos, con lo anterior se tiene el arco, que es la
suma ``vectorial'' de dos originales y que representa a la
rotación resultante. En general no conmutará la suma anterior
que es un resultado esperado ya que las matrices no conmutan bajo
la multiplicación.
La Fig (4.3) nos muestra una suma ``vectorial'' de esta clase



Next: Condición para obtener los
Up: Diversos aspectos de la
Previous: Representación geométrica
Contents
Pedro Hernandez
2006-02-20
![\begin{eqnarray*}
(\widehat{U} \times \widehat{V}, \widehat{U} \times \widehat{...
... v_{1} - u_{1} v_{3}) \ K + (u_{2} v_{1} - u_{1}
v_{2}) \ L])
\end{eqnarray*}](img460.png)
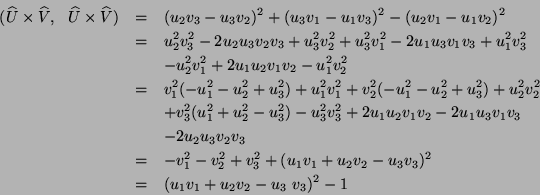
![\begin{displaymath}
(\widehat{U}, \widehat{W}) = [\widehat{U}, N \widehat{W}] =...
...egin{array}{c}
w_1 \\
w_2 \\
w_3
\end{array} \right]
\end{displaymath}](img474.png)
![\begin{displaymath}
N = \left[ \begin{array}{cccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array} \right]
\end{displaymath}](img475.png)