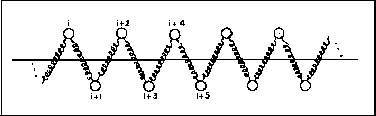Si
![]() , con
, con ![]() real resulta:
real resulta:
Por este resultado vemos que se multiplica por un factor, el
cual produce un cambio de signo, es decir, un desfasamiento de ![]() ,
por lo tanto se observarán oscilaciones con inversiones de fase;
además el comportamiento de las partículas alternantes es el
mismo, podemos pensar que las partículas que interaccionan a
segundos vecinos tienen un comportamiento similar esto lo podemos ver
de la siguiente forma:
,
por lo tanto se observarán oscilaciones con inversiones de fase;
además el comportamiento de las partículas alternantes es el
mismo, podemos pensar que las partículas que interaccionan a
segundos vecinos tienen un comportamiento similar esto lo podemos ver
de la siguiente forma:
Usando el hecho de que:
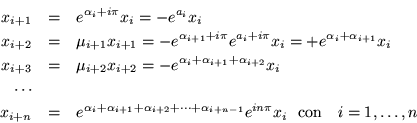
Analizando la forma general vemos que si ![]() es par, las
partículas:
es par, las
partículas:
![]() , se mueven en la misma forma,
podemos decir que van en la misma fase; si
, se mueven en la misma forma,
podemos decir que van en la misma fase; si ![]() es impar entonces las
partículas:
es impar entonces las
partículas:
![]() van en la misma fase,
gráficamente tenemos
van en la misma fase,
gráficamente tenemos