Si
![]() resulta:
resulta:
Por lo tanto en este caso, tendremos un movimiento ondulatorio
modulado por un factor exponencial que depende de la parte real de ![]() ;
por lo tanto si
;
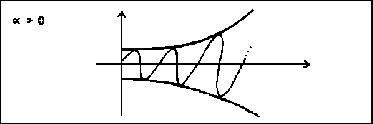
por lo tanto si ![]() , entonces
, entonces ![]() es una exponencial
creciente, este factor no es otra cosa que la amplitud que nos va a
modular la función ondulatoria, gráficamente.
es una exponencial
creciente, este factor no es otra cosa que la amplitud que nos va a
modular la función ondulatoria, gráficamente.
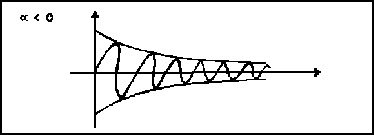
El caso en que ![]() , da lugar a una exponencial
decreciente, que también nos va a modular la función ondulatoria,
gráficamente tenemos.
, da lugar a una exponencial
decreciente, que también nos va a modular la función ondulatoria,
gráficamente tenemos.