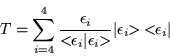 |
(2.32) |
Una vez obtenido, los eigenvalores y eigenvectores de la matriz
de transferencia, podemos emplear el ``teorema espectral'' (ref. [9]), el
cual nos dice que podemos expresar cualquier matriz en función de sus
eigenvalores y operadores de proyección, esto es, para el caso
particular que estamos tratando.
Ahora supongamos que tenemos dos eigenvalores distintos ![]() y
y ![]() y calculemos el producto interior
y calculemos el producto interior
![]() .
.
| (2.33) |
Supongamos que
![]() y analisemos que pasa
con el producto interior, con estos eigenvalores, por lo tanto de
(2.32) y (2.31) resulta:
y analisemos que pasa
con el producto interior, con estos eigenvalores, por lo tanto de
(2.32) y (2.31) resulta:
Como vemos este producto interior resulta distinto de cero por lo tanto podemos emplear el teorema espectral, para poder expresar, la matriz de transferencia a la enésima potencia.
Por otra parte, si el producto interior de dos eigenvectores con el mismo eigenvalor es distinto de cero, quiere decir que es posible formar un conjunto completo de eigenvectores, por lo tanto queremos investigar si con los eigenvectores de la matriz de transferencia, es posible obtener un conjunto completo de eigenvectores.
Calculemos el producto exterior.
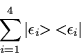
![\begin{displaymath}
Z=\left[\begin{array}{c} < \!\! 1\vert \\ < \!\! 2\vert \\ < \!\! 3\vert \\ \vdots \\ < \!\! n\vert \end{array}\right]
\end{displaymath}](img181.gif)
![\begin{displaymath}ZZ^{-1} = \left[\begin{array}{cccc}
<\!\! 1 \vert 1\!\! > &...
...t 2\!\! > & \ldots & <\!\! n \vert n\!\! >
\end{array}\right] \end{displaymath}](img183.gif)
Usando los resultados obtenidos en (2.34) y (2.35),
resulta que la matriz ![]() es completamente diagonal y cuyos elementos
no son otra cosa que los polinomios dados por (2.35) que son
polinomios distintos de cero, evaluados en las cuatro raíces,
esto es:
es completamente diagonal y cuyos elementos
no son otra cosa que los polinomios dados por (2.35) que son
polinomios distintos de cero, evaluados en las cuatro raíces,
esto es:
![\begin{displaymath}ZZ^{-1} =\left[\begin{array}{cccc}
\phi (\epsilon _1) & 0 &...
...3) & 0 \\
0 & 0 & 0 & \phi (\epsilon _4)
\end{array}\right] \end{displaymath}](img185.gif)
Estos elementos diagonales son distintos de cero, lo que implica que su determinante es distinto de cero, que es precisamente la condición de ``completamiento''.
Por otra parte el hecho de que la matriz de transferencia, tenga
un conjunto completo de eigenvectores, se puede apreciar también del
siguiente hecho; construimos el determinente ![]() cuyas columnas
son los eigenvectores de la matriz de transferencia y además la matriz
de este determinante, tiene por objeto diagonalizar la matriz de
transferencia esto es:
cuyas columnas
son los eigenvectores de la matriz de transferencia y además la matriz
de este determinante, tiene por objeto diagonalizar la matriz de
transferencia esto es:
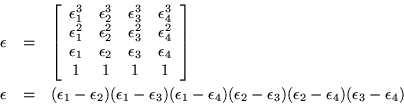
En donde
![]() y
y ![]() son las cuatro
raíces de la ecuación característica por otra parte, si
dos columnas son iguales, lo que quiere decir que dos raíces lo
sean, entonces tendremos dos columnas linealmente dependientes, lo
cual implica que el determinante es igual a cero; pero para el caso
en que estas raíces son distintas obtendremos que su solución
es el producto de todas las diferencias posibles de las raíces en
orden creciente como se puede apreciar en el determinante
son las cuatro
raíces de la ecuación característica por otra parte, si
dos columnas son iguales, lo que quiere decir que dos raíces lo
sean, entonces tendremos dos columnas linealmente dependientes, lo
cual implica que el determinante es igual a cero; pero para el caso
en que estas raíces son distintas obtendremos que su solución
es el producto de todas las diferencias posibles de las raíces en
orden creciente como se puede apreciar en el determinante ![]() ; por
lo tanto como para el caso que estamos tratando las raíces son
todas diferentes, resulta que las columnas y por lo tanto los
eigenvectores, son linealmente independientes y con esto podemos
concluir que la matriz de transferencia tiene un sistema de
coordenadas formada por los eigenvectores.
; por
lo tanto como para el caso que estamos tratando las raíces son
todas diferentes, resulta que las columnas y por lo tanto los
eigenvectores, son linealmente independientes y con esto podemos
concluir que la matriz de transferencia tiene un sistema de
coordenadas formada por los eigenvectores.
Existen varios métodos para demostrar que la solución dada con
anterioridad es la correcta, una de ellas consiste en que la forma
general del determinante ![]() , está dado por el determinante de
Vandermonde (ver apéndice A), otra consiste de un método de
solución directa, en ésta empleamos el hecho de que podemos
restarle a una columna otra sin que el determinante se altere.
, está dado por el determinante de
Vandermonde (ver apéndice A), otra consiste de un método de
solución directa, en ésta empleamos el hecho de que podemos
restarle a una columna otra sin que el determinante se altere.
Es conveniente mencionar que con el eigenvector renglón
![]() podemos construir el determinante siguiente:
podemos construir el determinante siguiente:
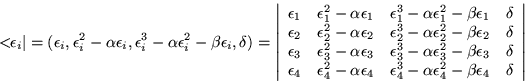
El cual, después de ciertas multiplicaciones, se nos reduce al
mismo determinante ![]() .
.
Otro resultado que es conveniente mencionar, está relacionado
con el producto interior
![]() y que consiste en lo
siguiente:
y que consiste en lo
siguiente:
Si al polinomio dado por (2.36) le sumamos un cuatro por
cero, es decir:
Si
![]() la ecuación anterior, es distinta de cero,
ya que vamos a suponer que la ecuación característica no tiene
raíces repetidas, por lo tanto
la ecuación anterior, es distinta de cero,
ya que vamos a suponer que la ecuación característica no tiene
raíces repetidas, por lo tanto
![]() y
y
![]() no son
cero evaluadas en el mismo punto.
no son
cero evaluadas en el mismo punto.
Otro resultado que falta obtener, para poder hacer la
sustitución completa en la ecuación (2.32) es el producto
exterior.
Por lo tanto, si sustituimos las ecuaciones (2.37) y
(2.38) en (2.32) obtendremos la forma de la matriz de
transferencia explícitamente en función de sus eigenvalores y
eigenvectores. La importancia de este resultado, es que nos permite
calcular la matriz de transferencia a la enésima potencia simplemente
elevando los eigenvalores, es decir

Esto es un resultado que se puede demostrar fácilmente, haciendo
uso de algunos resultados anteriores, por ejemplo calculemos ![]() para
el caso más general.
para
el caso más general.
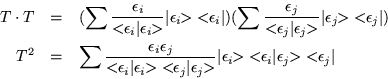
Empleando el resultado obtenido en (2.35) vemos que
únicamente los productos exteriores no cruzados serán distintos de
cero, es decir, empleamos la ortogonalidad de nuestros eigenvectores;
por lo tanto ![]() será distinto de cero en el caso de que
será distinto de cero en el caso de que ![]() , con
lo que resulta.
, con
lo que resulta.
Y así sucesivamente podemos hacer el cálculo para potencias más altas, lo cual no es necesario hacer en este trabajo ya que su demostración completa se encuentra en ref. [10], una observación que podemos hacer de este resultado, es que los productos exteriores son operadores idempotentes.