Ecuación característica para $\mu$, propiedades de la matriz de transferencia.

Nos interesa conocer los factores de propagación $\mu$, por lo cual calculamos la ecuación característica de la matriz de transferencia $T$, esto es:

$$\left[\begin{array}{cccc} \frac{-a_1}{a_2}-\mu & \frac{\l... ... & 1 & -\mu & 0 \\ 0 & 0 & 1 & -\mu \end{array}\right] = 0$$

Explícitamente:

$$\mu^4 +\frac{a_1}{a_2}\mu^3 +\frac{(a_0 -\lambda)}{a_2}\mu^2 +\frac{a_1}{a_2}\mu + 1 = \chi (\mu) = 0$$ (2.21)

Si hacemos $\mu = 1/\nu$ y la sustituimos en (2.21) resulta

$$\frac{1}{\nu^4} +\frac{a_1}{a_2}\frac{1}{\nu^3} +\frac{(a_0... ...ambda)}{a_2}\frac{1}{\nu^2} +\frac{a_1}{a_2}\frac{1}{\nu} +1=0$$ (2.22)

Ahora bien $a_2\neq 0$ en principio, ya que sino lo fuera estaríamos tratando con interacciones a primeros vecinos, además el factor constante de un polinomio es el producto de todas las raíces del polinomio, como el polinomio característico que nos resultó tiene el factor constante distinto de cero, esto quiere decir que ninguna de las raíces del polinomio es cero, entonces es posible decir que una de las raíces es de la forma $\mu = 1/\nu$ así si multiplicamos a (2.22) por $\nu^4$, tenemos.

$$1+\frac{a_1}{a_2}\nu +\frac{(a_0 -\lambda)}{a_2}\nu^2 +\frac{a_1}{a_2}\nu^3 +\nu^4 - \chi (\nu) =0$$

Analizando esta última ecuación, vemos que es exactamente de la misma forma que la ecuación (2.21); de esto deducimos un resultado interesante que nos permite afirmar que sí, una de las raíces es $\mu$ entonces otra de las raíces es $1/\mu$, es decir:

Si $\chi (\mu) = 0 \ \rightarrow \ \chi (1/\mu )=0$.

Por lo tanto todas las raíces del polinomio característico ocurren en parejas recíprocas, existiendo dos casos degenerados que corresponden al valor ``1'' y al ``O'' que no tienen recíproco.

Supongamos que $\epsilon ,1/\epsilon ,\zeta$ y $1/\zeta$ son raíces del polinomio característico, por lo tanto podemos escribir que:

$$a_2 (\mu -\epsilon ) \: (\mu -1/\epsilon )\: (\mu -\zeta)\: (\mu -1/\zeta)\: =\:0$$

Efectuando un producto parcial adecuado resulta:

$$[\mu^2 -\mu(\epsilon +1/\epsilon ) +1]\: [\mu^2 -\mu(\zeta +1/\zeta) +1] \: =\: 0$$

definiendo:

$$\epsilon +1/\epsilon = a \qquad \mbox{ y } \qquad \zeta + 1/\zeta = b$$ (2.23)

efectuando el producto y agrupando términos semejantes, resulta finalmente:

$$\mu^4-(a+b)\mu^3 +(2+ab)\mu^2 -(a+b)\mu + 1= 0$$ (2.24)

Si comparamos las ecuaciones (2.21) y (2.23) e igualamos los coeficientes, resultan las siguientes ecuaciones.

$$a+b = -\frac{a_1}{a_2} =\alpha = \gamma$$ (2.25)

$$2+ab = \frac{a_0 -\lambda}{a_2} = -\beta$$ (2.26)

Con este sistema de ecuaciones acopladas, es posible encontrar la suma de un par de raíces recíprocas $\mu$, en la siguiente forma: despejemos de (2.24) $b$ y sustituyámoslo en (2.25), con lo que se tiene

$$a^2 -\alpha a -(2+\beta) = 0$$

En donde las soluciones de esta ecuación cuadrática en ``$a$'' son:

$$a= \frac{\alpha\pm \sqrt{\alpha^2 +4(2+\beta)}}{2}$$ (2.27)

En donde se tiene explícitamente a ``$a$'' en términos de los coeficientes $\alpha$ y $\beta$ que son conocidos, con esta última ecuación podemos calcular una raíz individual $\epsilon$, para lo cual empleamos la definición de ``$a$'', esto es:

$$\begin{eqnarray*} a & = & \epsilon +1/\epsilon \ \mbox{ lo cual desarrollado resulta:} \\ \epsilon ^2 - \epsilon a+1 & = & 0 \end{eqnarray*}$$

y finalmente esta ecuación cuadrática tiene por soluciones:

$$\epsilon = \frac{a}{2}\pm \sqrt{(a/2)^2 -1}$$ (2.28)

si definimos $a/2 =\cos\phi$, lo cual es una sustitución usual, se obtiene

$$\epsilon =\cosh \,\phi +\,{\mbox{senh}}\,\phi =e^{\pm \phi}$$

que es un resultado usado con anterioridad.

Por lo tanto podemos garantizar que las ondas se suceden en parejas, entonces en el movimiento a través de una cadena, una componente aumenta y la otra disminuye, ya que ocurren en parejas recíprocas, por el comportamiento de nuestras ondas podemos decir que se trata de ondas parciales, que son ondas limitadas en el espacio. Lo importante es que para cada onda que crezca hay otra que disminuye, ya que la matriz es real su polinomio característico tiene coeficientes reales, podemos asegurar que si sus raíces son complejas y si la conjugada y la recíproca conjugada son diferentes, entonces resultará que el número de onda es imaginario puro; esto nos da una diferencia con respecto al caso de interacción a primeros vecinos en donde resulta que la conjugada y su recíproca son iguales.

O sea siempre existe oscilación con amplitud constante aún cuando la fase cambie y tengamos ondas crecientes y decrecientes, ya que el factor de fase es siempre 1, como es sabido a las ondas de esta naturaleza se les llama ondas estacionarias.

Es necesario mencionar que para interacciones a vecinos más lejanos, no podemos asegurar que una conjugada y su recíproca sean iguales, probablemente sean distintas, en cuyo caso tendremos las llamadas ondas superficiales; es característico cuando hay interacciones a vecinos lejanos, que existan vibraciones de ondas confinadas sólo a la superficie.

Una vez obtenidas las ecuaciones que nos dan las raíces individuales esto es las frecuencias espaciales, podemos proceder a encontrar la forma de los eigenvectores en términos de estas raíces individuales, esto es.

Para el cálculo del eigenvector columna, supongamos que $a,b,c$ y $d$ son las componentes de este vector, por lo tanto podemos formar el sistema de eigenvalores siguiente:

$$\left[ \begin{array}{cccc} \alpha & \beta & \gamma & \delt... ...n \left[\begin{array}{c} a \\ b \\ c \\ d \end{array}\right]$$

desarrollando los productos indicados resulta

$$\left. \begin{array}{l} \alpha a+\beta b+\gamma c+\delta d=... ... b \\ b =\epsilon c \\ c =\epsilon d \end{array}\right\}$$ (2.29)

Por conveniencia y como siempre es posible hacerlo definamos $d=1$ con lo que resulta

$$a=\epsilon ^3 ,\ b=\epsilon ^2 ,\ c=\epsilon ^1 \ \mbox{ y }\ d=\epsilon ^0$$

Por lo tanto con estos valores tenemos la forma del eigenvector además es conveniente introducir la notación de ``KET'' (ver ref. [8]), para el $i$-ésimo eigenvector columna de la matriz de transferencia, correspondiente al eigenvalor $\epsilon _i$, esto es

$$\vert\epsilon _i \!\! > \: =\: \left[\begin{array}{c} \ep... ...on _i^2 \\ \epsilon _i^1 \\ \epsilon _i^0 \end{array}\right]$$ (2.30)

Sustituyendo los valores obtenidos de $a,b,c$ y $d$ en la primera de las ecuaciones (2.29) resulta

$$\alpha\epsilon ^3 +\beta\epsilon ^2 +\gamma\epsilon +\delta =\epsilon ^4$$ (2.31)

lo cual como vemos, nos reproduce la ecuación característica (2.21) lo cual implica, la consistencia con las demás ecuaciones.

Ahora calculemos los eigenvectores renglón, para lo cual supongamos que $(a,b,c,d)$ es un vector con componentes a ser determinadas, esto es:

$$[a,b,c,d]\left[\begin{array}{cccc} \alpha & \beta & \gamma & ... ... 0 \\ 0 & 0 & 1 & 0 \end{array}\right] = \epsilon [a,b,c,d]$$

explícitamente tenemos

$$\begin{eqnarray*} a\alpha +b=\epsilon a \\ a\beta +c=\epsilon b \\ a\gamma +d=\epsilon c \\ a\delta = \epsilon d \end{eqnarray*}$$

tomando por conveniencia $a=1$, tenemos

$$d=\delta/\epsilon \, ;\ \ b=\epsilon -\alpha \ \ \mbox{ y }\ \ c=\epsilon (\epsilon -\alpha) -\beta$$

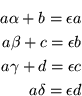
Con estos valores el $i$-ésimo eigenvector renglón, usando la notación del ``bra'' toma la forma siguiente:

$$<\epsilon _i \vert=[1, \epsilon -\alpha, \ \epsilon(\epsilon -\alpha)-\beta, \ \delta/\epsilon ]$$

Es conveniente ponerlo en una norma más adecuada, para lo cual multiplicamos por $\epsilon$, esto es:

$$<\epsilon _i \vert=[\epsilon , \ \epsilon^2 -\epsilon \alph... ... \epsilon ^3 -\epsilon ^2\alpha -\epsilon \beta , \ \delta ]$$