Forma del sistema inhomogéneo.

Ahora vamos a analizar el caso que da lugar a un sistema inhomogéneo y al mismo tiempo analizaremos como se modifica nuestro modelo.

Así que vamos a analizar un sistema de la forma:

$$\frac{d^2 x}{dt^2} =\left[\begin{array}{cccccccc} a_0 & a... ...}{c} f_1 \\ f_2 \\ f_3 \\ \vdots \\ f_n \\ \end{array}\right]$$ (8.1)

Como se puede ver vamos a aplicarle fuerzas a cada partícula, estas fuerzas dependerán únicamente del tiempo, pero como llevan subscritos podemos pensar que también dependen de las coordenadas.

Existe un caso de interés, el cual da lugar a un sistema de ecuaciones diferenciales de la forma anterior, este caso es el de una cadena diatómica, es decir una cadena formada por partículas de dos clases diferentes, generalmente formada de iones, por ejemplo podemos considerar la estructura del NaCl cuya cadena podemos considerarla que está formada de la siguiente manera:

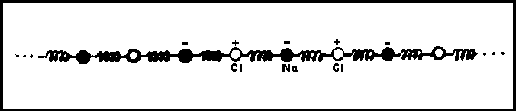
Entonces estos iones en el campo de una onda electromagnética sienten ciertas fuerzas orientadas en la dirección del campo o en contra, de acuerdo con los signos de sus cargas, o sea que si le aplicamos un campo electrostático a la cadena diatómica, los iones positivos se moveran en una dirección y los negativos en la otra dirección, por lo tanto tenemos una fuerza aplicada a cada partícula, dicha fuerza dependerá posiblemente del tiempo, o sea éste es un modelo que nos permite analizar los efectos de un sólido sobre el cual incide una onda electromagnética por ejemplo radiación infrarroja, así que las respuestas a estos campos son vibraciones excitadas que son descritas por un sistema de ecuaciones con un término de fuerza adicional, en la forma indicada por el sistema de ecuaciones diferenciales.

Otro caso que produce vibraciones importantes y que tiene que ver más con la rama acústica, que con la óptica, es el que resulta de aplicar una fuerza sinosoidal únicamente a un extremo de la cadena y lo que deseamos determinar es que tipo de fuerza o como es modificada una fuerza al llegar al otro extremo, por lo tanto queremos ver que tipo de fuerzas son aplicadas y ver si una onda acústica llega al otro extremo o no.

Para solucionar el problema es necesario encontrar nuestra relación de recurrencia, la cual para el interior de la cadena tendrá la forma:

$$\frac{d_2 x_i}{dt} =a_2 x_{i+2} +a_1 x_{i-1} +a_0 x_i +a_2 x_{i-2} +a_1 x_{i-1} +f_i (t)$$ (8.2)

Como se puede apreciar, la diferencia de esta ecuación con respecto a la cadena normal (ec. 2.$4'$) está dada por la fuerza $f_i (t)$ la cual puede extenderse con el tiempo.

Por lo tanto no es mucha la diferencia con respecto a sistemas ordinarios y de la misma forma como se soluciona un sistema inhomogéneo con ayuda del homogéneo, se tratará de encontrar la solución.

Por lo tanto vamos a suponer que el vector $x$ es un eigenvector, es decir, representa un posible desplazamiento, en el caso de que exista otro tipo de desplazamiento formaremos una combinación de ellos ya que es un problema lineal, o sea podemos combinar los modos normales de vibración representados por los eigenvalores, además vamos a estudiar el movimiento general usando condiciones iniciales arbitrarias en términos de eigenfunciones.

Por lo tanto reescribiendo (8.2) empleando los conceptos anteriores y las condiciones suplementarias, resulta:

$$x_{i+2} = -\frac{a_1}{a_2} x_{i+1} -\frac{\lambda -a_0}{a_2} x_i -\frac{a_1}{a_2} x_{i-1} -\frac{a_2}{a_2} x_{i-2} -\frac{1}{a_2} f_i (t)$$ (8.3)

$$x_{i+1} = x_{i+1}$$

$$x_i = x_i$$

$$x_{i-1} = x_{i-1}$$

Por otra parte los modos normales, que son los eigenvectores (por definición) forman una base, debido a que estamos tratando con matrices simétricas, por lo tanto podemos postular no que $(A-\lambda II)X=0$, pero si postulamos que para cualquier potencia de $k$ se cumple que $(A-\lambda II)^k X=0$, lo cual define los eigenvectores; además entre el conjunto de eigenvectores, existe un conjunto completo y en base a esto, es en donde sacamos cualquier vibración, como un modelo normal de vibración, por otra parte en los eigenvectores el tiempo es separable, ya que tenemos un factor que depende del tiempo dado por $e^{i\omega t}$ multiplicados por un factor que depende del espacio, o sea, podemos decir que los eigenvectores forman un tipo de movimiento donde es separable el tiempo, además la base así formada es sumamente deseada, es por tanto, tan importante diagonalizar la matriz y obtener sus eigenvalores, porque con esta técnica un problema de $n$ dimensiones se reduce a un problema de una dimensión que es mucho más sencilla de solucionar.

En forma matricial el sistema de ecuaciones (8.3) resulta

$$\left[\begin{array}{l} x_{i+2} \\ x_{i+1} \\ x_i \\ x_{i-1}... ...t[\begin{array}{c} -f_i /a_2 \\ 0 \\ 0 \\ 0 \end{array}\right]$$ (8.4)

Que es la forma matricial de recurrencia que resultó anteriormente, excepto una cantidad que representa la fuerza sobre la partícula $i$-ésima.

Con objeto de solucionar (8.4) definamos las siguientes cantidades:

$$x_i =\left[\begin{array}{l} x_{i+1} \\ x_i \\ x_{i-1} \\ x_... ...y}{l} x_{i+2} \\ x_{i+1} \\ x_i \\ x_{i-2} \end{array}\right]$$

Y también definimos el vector de fuerza como $F_i$ y la matriz de transferencia como $T_d$.

Con lo cual (8.4) toma la forma

$$x_{i+1} = T_d x_i +F_i$$

Desarrollando para algunas $i$'s, por ejemplo

$$\begin{eqnarray*} i=1 & \rightarrow & X_2 =T_d X_i +F_1 \\ i=2 & \rightarrow ... ..._n =T_d^n X_1 +T_d^{n-1}F_1 +T_d^{n-2}F_2 +T_d^{n-3}F_3 +\cdots \end{eqnarray*}$$

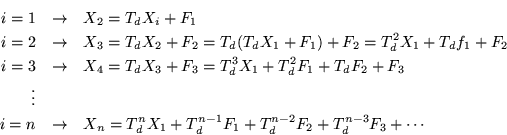
Esta última ecuación la podemos poner finalmente como:

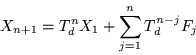$$X_{n+1} =T_d^n X_1 +\sum_{j=1}^n T_d^{n-j} F_j$$ (8.5)

Como vemos la solución obtenida tiene bastante similitud con la solución general que se obtiene en un sistema inhomogéneo (ver. Ref[13]) y que está dada por

$$X(t) =\Omega (t,t_0) X(t_0) +\int_{t_0}^t \Omega (t,\sigma) F(\sigma) d\sigma$$ (8.6)

En donde su derivación es exactamente igual, a la efectuada para el caso que estamos tratando, la única diferencia es que aquí queda finita la solución y en el otro caso hemos pasado a un límite, razón por la cual reemplaza a la integral una suma; además debido a que $\Omega (t,t_0)$ es el producto de todas las matrices con tiempo variable, no es muy difícil encontrar las fuerzas aplicadas a la vibración de una cadena por medio de la técnica que da la solución (8.6), lo único que tenemos que hacer, es expresar la influencia de una fuerza sobre una partícula en el movimiento de otra partícula y esta influencia se expresa por un producto de las $n$'s correspondientes a la distancia en donde queremos aplicar la fuerza y en donde queramos observar los resultados.

Además posteriormente deduciremos una transformación, que nos permite emplear la ecuación de movimiento $M$, para poder calcular el espectro de frecuencias y los modos normales de vibración correspondientes.