Consideremos una cadena unidimensional monoatómica, formada por
masas equidistantes ![]() y constantes de resorte
y constantes de resorte ![]() , esto es:
, esto es:
En donde la serie: ![]() nos denotará la colocación
de las partículas y la serie:
nos denotará la colocación
de las partículas y la serie:
![]() nos denotará
sus desplazamientos, relativos a su posición de equilibrio.
nos denotará
sus desplazamientos, relativos a su posición de equilibrio.
Por otra parte, los resortes que consideramos son elásticos, de
tal forma que si ![]() y
y ![]() son los desplazamientos (que
consideramos transversales) de las masas sucesivas, en sus posiciones
de equilibrio, entonces la fuerza debida a interacciones a segundos
vecinos, entre la partícula
son los desplazamientos (que
consideramos transversales) de las masas sucesivas, en sus posiciones
de equilibrio, entonces la fuerza debida a interacciones a segundos
vecinos, entre la partícula ![]() -ésima y sus dos vecinas más
próximas, por la derecha e izquierda es, aplicando la ley de Hooke.
-ésima y sus dos vecinas más
próximas, por la derecha e izquierda es, aplicando la ley de Hooke.
En donde ![]() y
y ![]() son las constantes de fuerza asociadas con
interacciones de fuerza central a primeros y segundos vecinos
respectivamente.
son las constantes de fuerza asociadas con
interacciones de fuerza central a primeros y segundos vecinos
respectivamente.
La fuerza descrita por la ecuación (2.1), depende
linealmente del desplazamiento relativo de las partículas,
entonces si movemos todo el resorte, éste no producirá una fuerza
del tipo que queremos analizar, pero si movemos las partículas
relativas una a otra obtendremos una fuerza, por lo tanto analizaremos
como por ejemplo, un desplazamiento en la partícula ![]() , va a
producir una fuerza en la partícula
, va a
producir una fuerza en la partícula ![]() , es claro que además
existen otros tipos de fuerzas que no serán descritas por nuestras
ecuaciones de movimiento, como son las debidas a un campo
electrostático, estas fuerzas se involucran en un modelo mucho más
realista como es el de polímeros y sólidos, también es claro
que aunque es una hipótesis muy sencillo suponer que únicamente
existen fuerzas debidas a interacciones entre las partículas, es
adecuado para muchas aplicaciones.
, es claro que además
existen otros tipos de fuerzas que no serán descritas por nuestras
ecuaciones de movimiento, como son las debidas a un campo
electrostático, estas fuerzas se involucran en un modelo mucho más
realista como es el de polímeros y sólidos, también es claro
que aunque es una hipótesis muy sencillo suponer que únicamente
existen fuerzas debidas a interacciones entre las partículas, es
adecuado para muchas aplicaciones.
Usando la segunda ley de Newton, tenemos que la fuerza actuando
sobre la partícula ![]() -ésima está dado por:
-ésima está dado por:
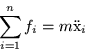 |
(2.2) |
De lo anterior podemos notar, que la distancia entre las
partículas, es decir, la constante de la red no entra
explícitamente en las ecuaciones (2.1) ya que su efecto
está involucrado en las constantes de fuerza; por otra parte con esta
ecuación es posible calcular las ecuaciones de movimiento de todas
las partículas que se encuentren en el interior de la cadena; para
las partículas de los extremos, las ecuaciones de movimiento están
dadas por:
Para la partícula del extremo izquierdo
Para la partícula del extremo derecho. Es conveniente
definir las siguientes cantidades:
Por lo tanto con este modelo físico, llegamos a un sistema
de ecuaciones diferenciales que en forma matricial, lo podemos escribir
como:
![\begin{displaymath}
\frac{d^2}{dt^2} \left[\begin{array}{l} x_1 \\ x_2 \\ x_3 \...
...ray}{l} x_1 \\ x_2 \\ x_3 \\ : \\ : \\ x_n \end{array}\right]
\end{displaymath}](img25.gif) |
(2.6) |
Por lo tanto vemos, que para este caso particular, las ecuaciones de movimiento dan lugar a un sistema de ecuaciones diferenciales, en donde la matriz de los coeficientes que resulta de forma pentagonal nos denotará la matriz de movimiento de la cadena. Matemáticamente el problema en resolver el sistema de ecuaciones diferenciales está involucrado en la matriz de movimiento, por lo cual se hace necesario dedicarle un estudio especial.
Es necesario mencionar que aunque en este momento, es nuestra intención discutir la formulación matemática para el interior de cualquier cadena, tenemos que emplear conceptos del caso de una cadena con extremos fijos Fig. 1, que puede ser considerada como el interior de una cadena, lo mismo que el modelo del anillo, que son algunos de los modelos que analizaremos posteriormente (Cap. 6 y Cap. 5 respectivamente).