Solución del determinante ![]() , definido como:
, definido como:
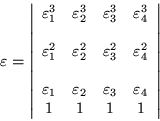
La forma general de este determinante, está dado por el
determinante de Vandermonde, esto es:
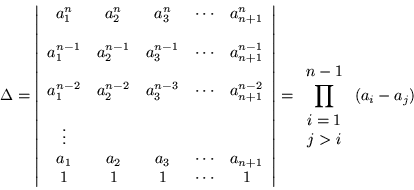
Para demostrar este resultado, nos basamos en una propiedad de los determinantes, lo cual nos permite multiplicar cualquier renglón del determinante por un escalar y sumarlo o restarlo a otro sin cambiar el valor del determinante, lo que en realidad se trata de hacer, es poner el determinante en forma diagonal, para esto es necesario que los elementos de este determinante diagonal, sean polinomios mónicos es decir, polinomios en los que el coeficiente de la potencia más alta es uno.
Multipliquemos el determinante por los coeficientes
![]() en la forma siguiente:
en la forma siguiente:

Sumando los renglones que se multiplicaron, al primer renglón,
resulta que cada elemento del primer renglón, está formado por
polinomios mónicos, es decir polinomios mónicos ![]() de grado
de grado
![]() , evaluados en los puntos
, evaluados en los puntos
![]() .
.
Estos polinomios mónicos son de la forma.
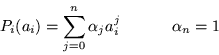
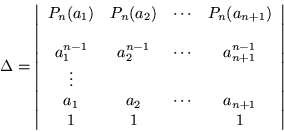
Aplicando la misma técnica, para obtener los elementos del
segundo renglón como polinomios mónicos
![]() de
grado
de
grado ![]() que deseamos evaluar en los puntos
que deseamos evaluar en los puntos
![]() , es decir, por sumar múltiplos de los
demás renglones, al segundo renglón se obtiene:
, es decir, por sumar múltiplos de los
demás renglones, al segundo renglón se obtiene:
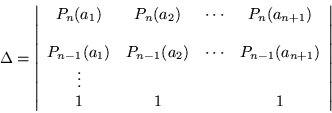
En general, en el ![]() -ésimo renglón son construidos
polinomios mónicos de grado
-ésimo renglón son construidos
polinomios mónicos de grado ![]() ; la dimensión de la matriz
es
; la dimensión de la matriz
es ![]()
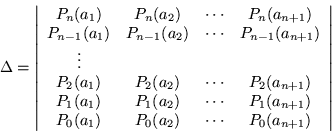
Escojamos el desarrollo siguiente:
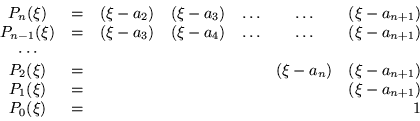

Por lo tanto el determinante toma finalmente la forma:
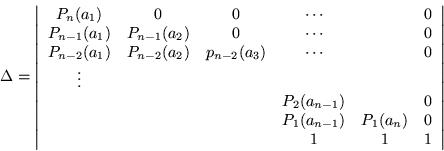
Por lo tanto, como queda un determinante triangular, éste no es otra cosa que el producto de su diagonal principal, o sea:
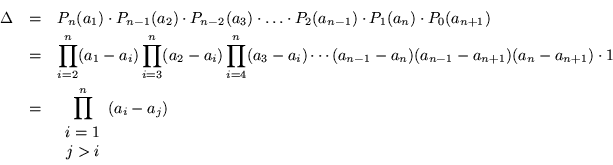
Que es el valor tradicional del determinante de Vandermonde.